background-image: url(https://upload.wikimedia.org/wikipedia/en/5/53/Michigan_State_University_seal.svg) background-position: 10% 95% background-size: 12% class: inverse left top # Leveraging Differentiation of Persistence Diagrams for Parameter Space Optimization and Data Assimilation ### **Max Chumley** <br> &mdash; <br> Mechanical Engineering<br><br>Computational Mathematics<br>Science and Engineering<br> &mdash;<br>Date: 4-11-24 <!-- ------------------------------------------------------- --> <!-- DO NOT REMOVE --> <!-- ------------------------------------------------------- --> <!-- SET TITLE IMAGES HERE -- NOTE: :img takes 3 arguments: (width, left, top) to position the graphic.-->   ??? Today I will be presenting my proposed work on two novel applications leveraging differentiation of persistence diagrams. --- # Acknowledgements  ??? I would like to start by thanking the air force office of scientific research and the national science foundation for funding this work. I would also like to thank my collaborators shown here. --- # Road Map 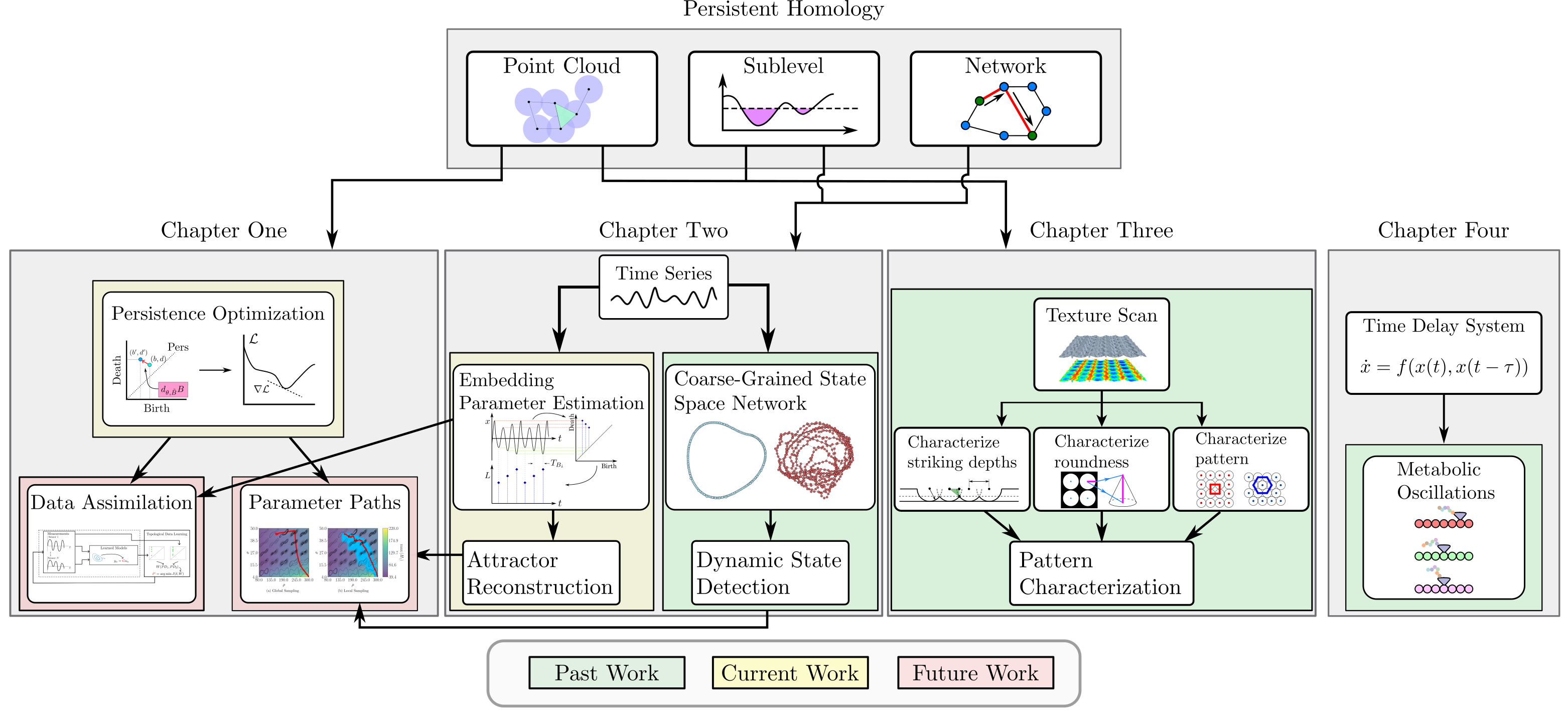 ??? Here is an overview of my research. Overall, my work is focused on using tools from Topological Data Analysis, in particular persistent homology, for the analysis of dynamical systems and time series data. My work is organized into four chapters and this talk today will mainly focus on the first chapter. I will start with an overview of the tools I use from topological data analysis and then show how to optimize functions of persistence along with my two proposed applications of this tool. I will then draw some connections to these methods by presenting my work on time series embedding and network representations. First, I will focus on the necessary background on topological data analysis and persistent homology. --  --- # Simplicial Complex and Homology  ??? Topological data analysis is a field that is focused on extracting shape or global structure information from data. Data can come in many forms and one common representation is a point cloud in R^n. The goal is to analyze the shape of this point cloud to draw conclusions about the underlying system that generated the data. To analyze shape we can look at a simplicial complex induced on the point cloud by fixing a connectivity parameter r and adding edges or 1-simplices when the euclidean distance between any two points is less than 2r and adding faces or 2-simplices when this is true for any set of three points. This concept can also be generalized to higher dimensional simplices. Here I have illustrated a simplicial complex called the Vietoris Rips complex but other simplicial complexes also exist that we will study more later. Once we have a simplicial complex induced on the data, we can say something about its shape by computing its homology. Homology gives a measure of structure in different dimensions. For example, in the figure here there is a 0D homology class as a connected component and a 1D homology class as a loop that has not closed in the simplicial complex. We can also have higher dimensional homology such as 2D which quantifies voids and so on. It is difficult to choose the connectivity parameter that will result in optimally extracting topological information from the data. To avoid this choice, we instead study a changing simplicial complex or filtration where each successive complex includes the previous. Quantifying how the homology changes with respect to the connectivity parameter is called persistent homology. -- 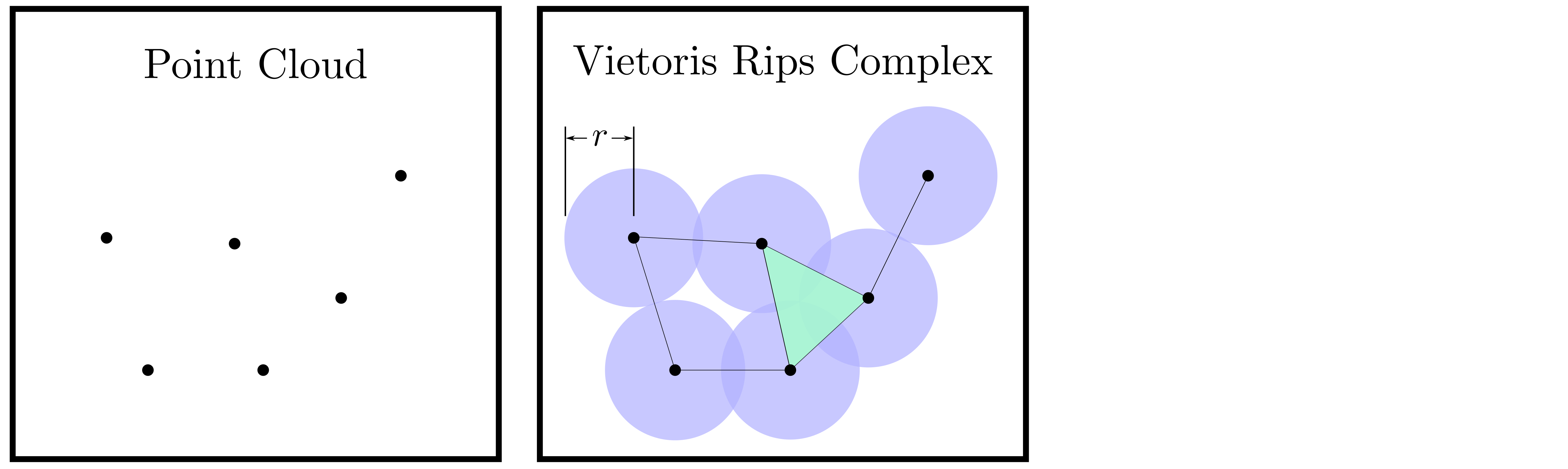 --  --- # Persistent Homology - Point Cloud   ??? We track the birth and death of homology classes in a persistence diagram by plotting the value of the connectivity parameter where that class is born as its x coordinate and the value where it dies as the y coordinate. It is helpful to imagine this process as centering a circle at each point in the point cloud and varying the radius of the circles to generate the persistence diagram. Here the data has a large loop structure with some noise and we see that as the connectivity parameter increases we have one persistence pair that is far from the diagonal and five other loops that are close to the diagonal meaning their birth and death times are close. The features close to the diagonal are often attributed to noise in the data and points far from the diagonal indicate prominent structures. --   --   --- # Persistent Homology - Sublevel  ??? We can also apply persistent homology to image data such as the one shown here. The filtration in this case changes from a simplicial complex to a cubical complex where instead of the building blocks being triangules and tetrahedra, we build our structure out of squares (pixels) or cubes (voxels). Then our filter function is a height function on the image instead of the distance between points. This is represented by the 3D surface here. This flavor of persistence is called sublevel persistence where we compute homology of sublevel sets of the surface. For example, in the image shown on the left here, we see that there are 6 components and 2 loops and as we change the height parameter each of the 6 components are born at different heights and die when they merge with an older component. It is helpful to imagine this process as filling the surface with water and when water over flows from one valley to another the components connect. In this animation of the sublevel persistence process we see that as the height increases, (or as water fills the surface) some of the components connect and we also see the two loops present in the 1D persistence diagram. --  --  -- 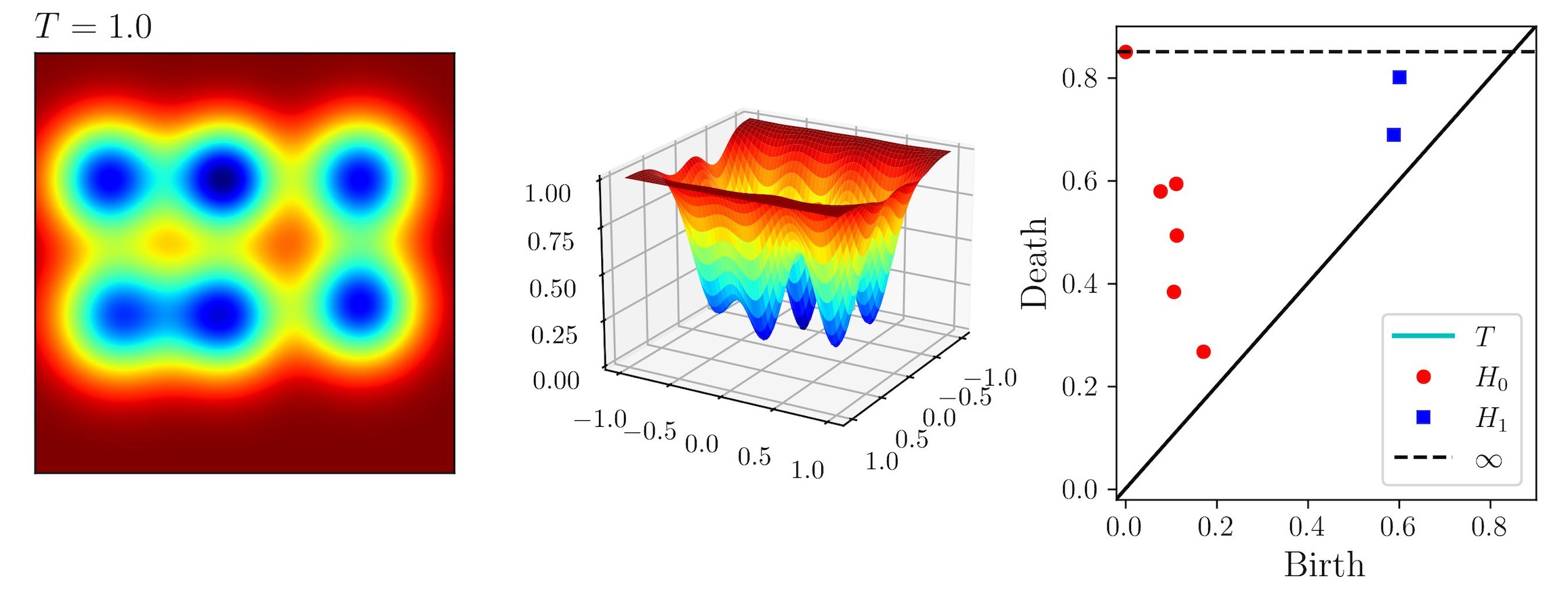 --- # Persistent Homology - Network 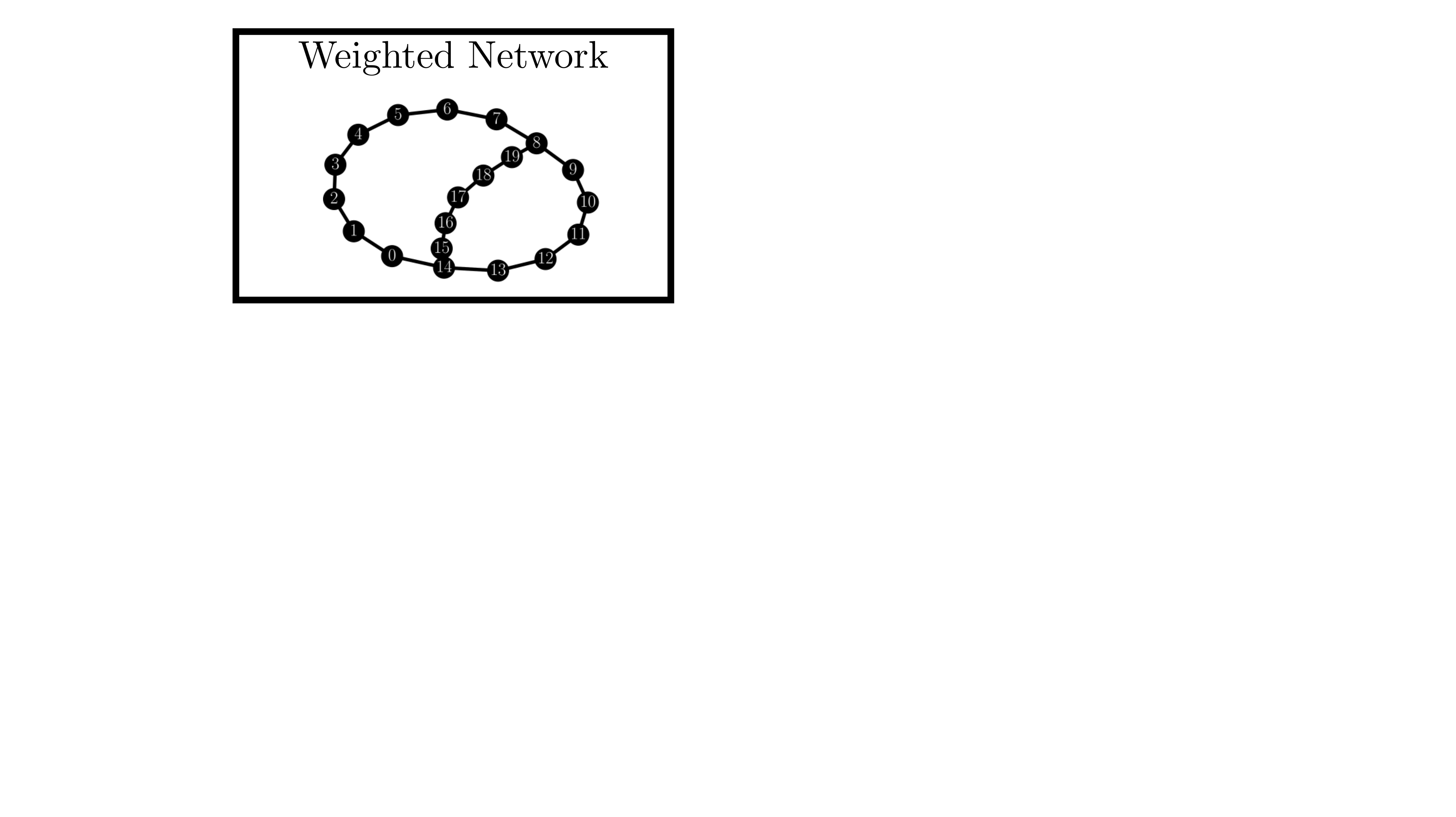 ??? The final flavor of persistence we will cover today is when our data is in the form of a weighted network. In the example here our network has two loops and we would like to quantify its topology using persistence. Network persistence requires a notion of distance on the network. One way of doing this is to use the shortest path distance between two vertices as shown here where the cost function C(P) is minimized to determine the path that minimizes the sum of the weights between two vertices. Doing this for all pairs of vertices in the network gives its corresponding distance matrix allowing for a simplicial complex to be induced on the network. We start with all of the vertices in the network and when the connectivity parameter reaches the shortest path distance between two vertices we add an edge in the simplicial complex. At this point we see the two loops are born. As we increase the connectivity parameter the loops fill in just as was done in point cloud persistence but with the important distinction of the different notion of distance between vertices. Using this process, we compute the persistence diagram of the network using the shortest path distance metric. -- 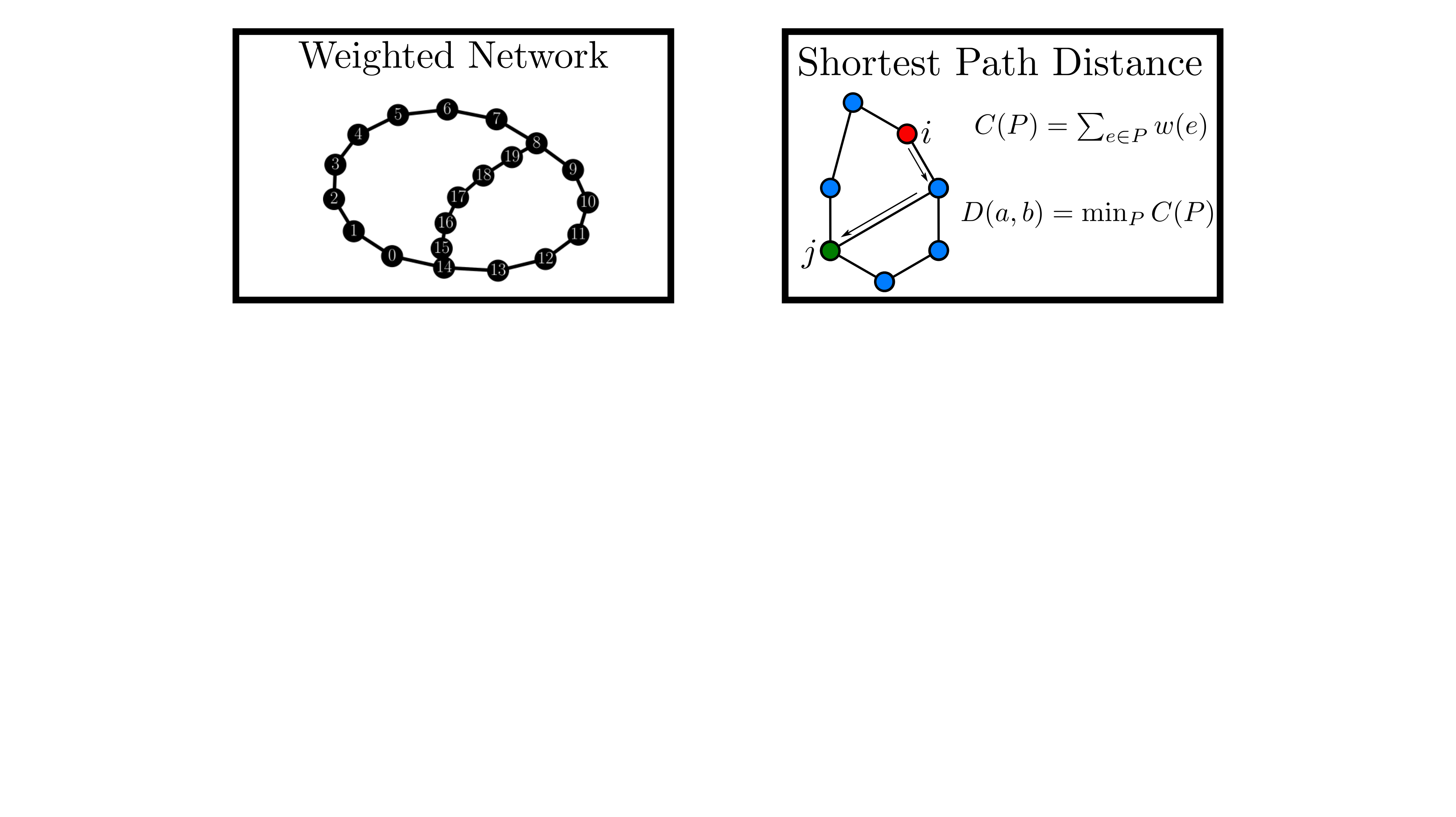 -- 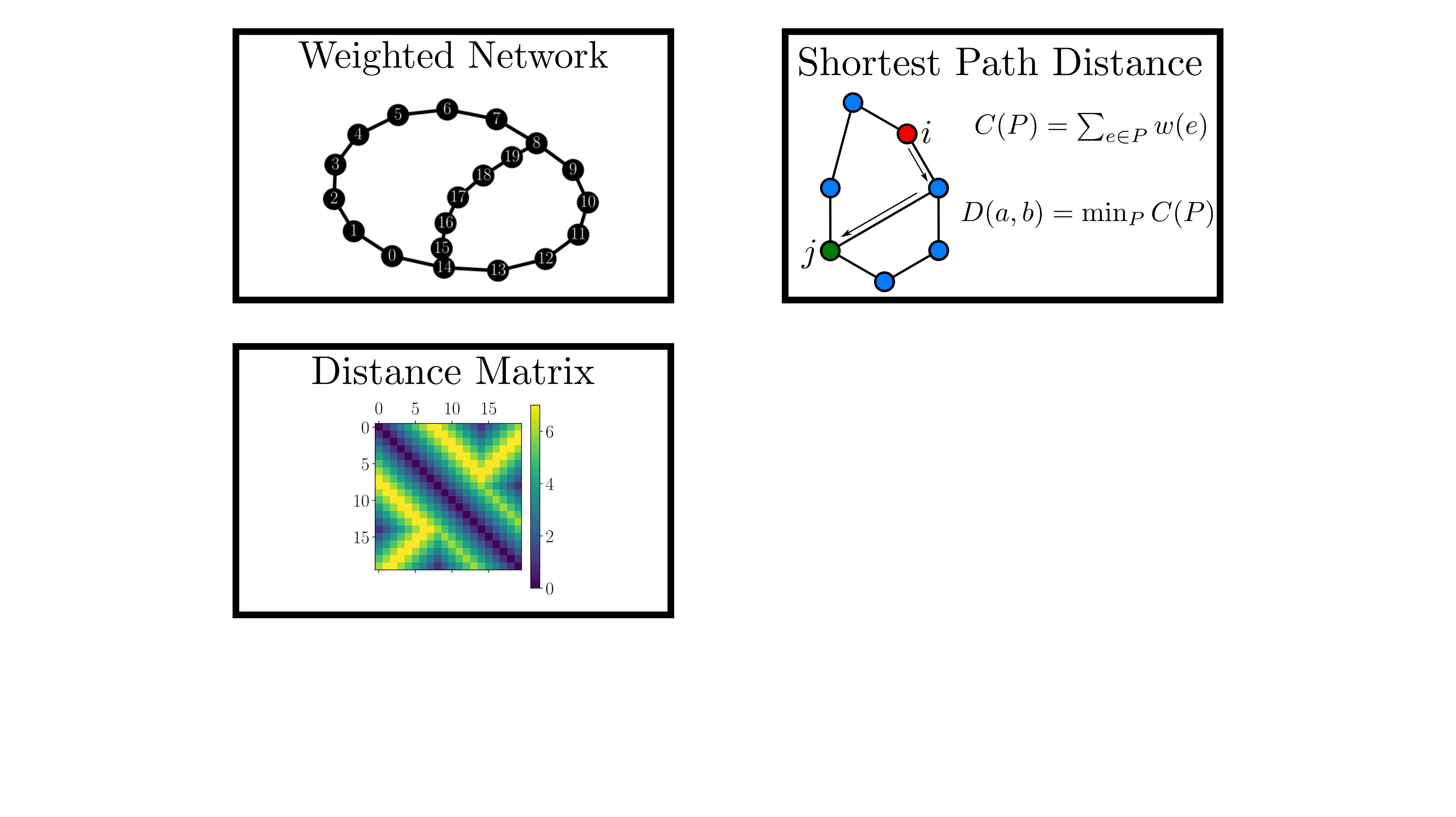 --  --  --  -- 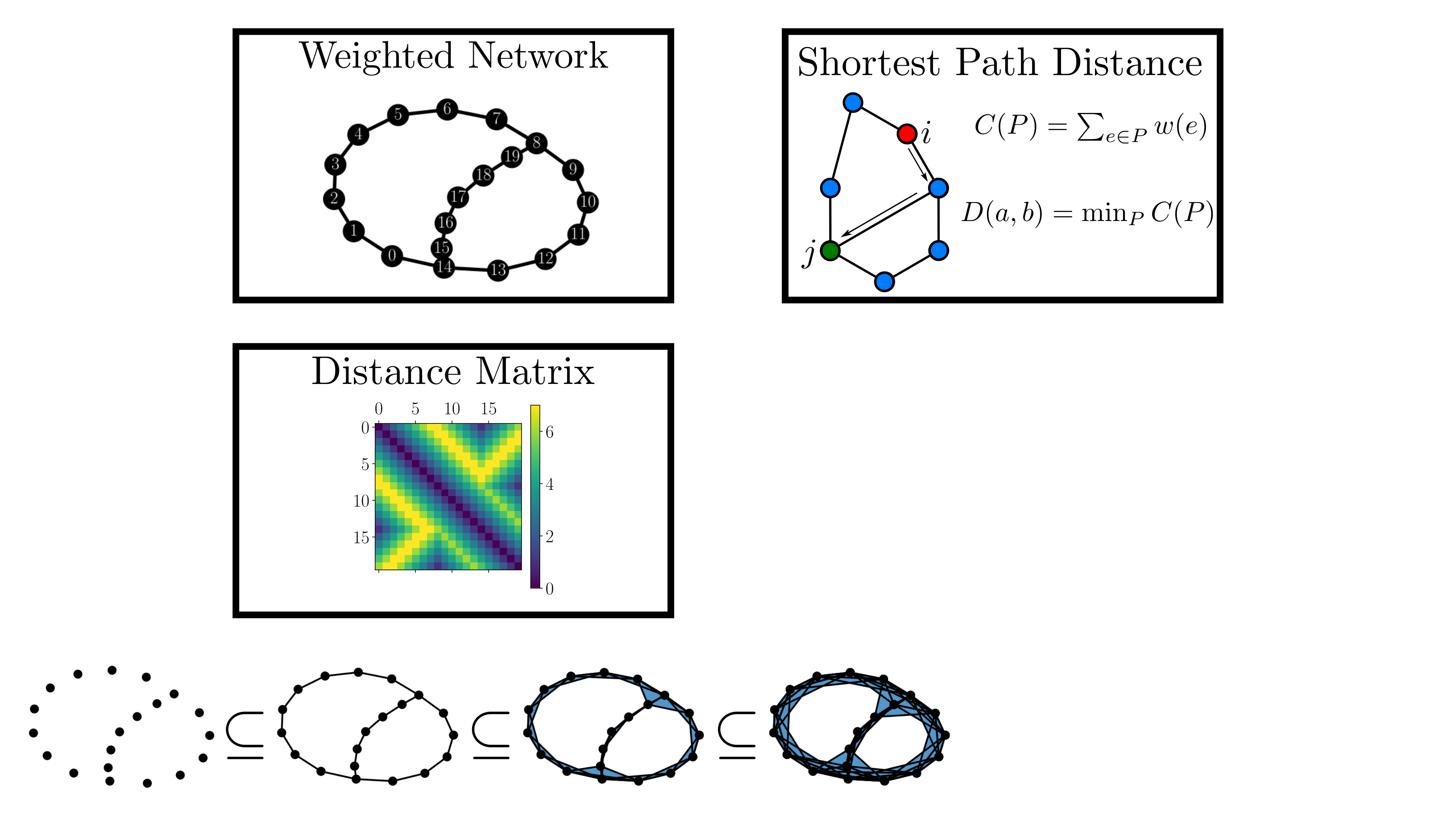 -- 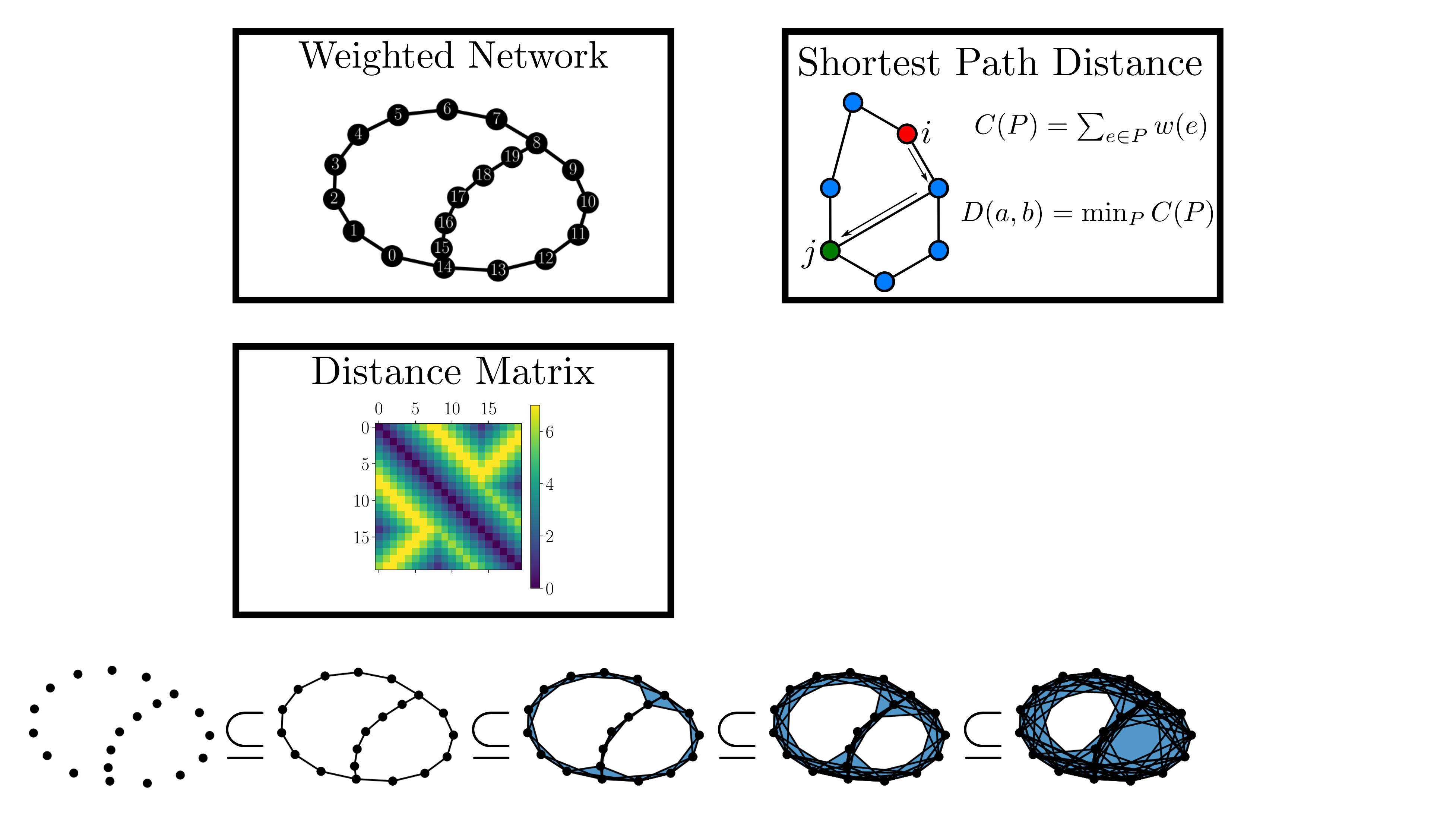 -- 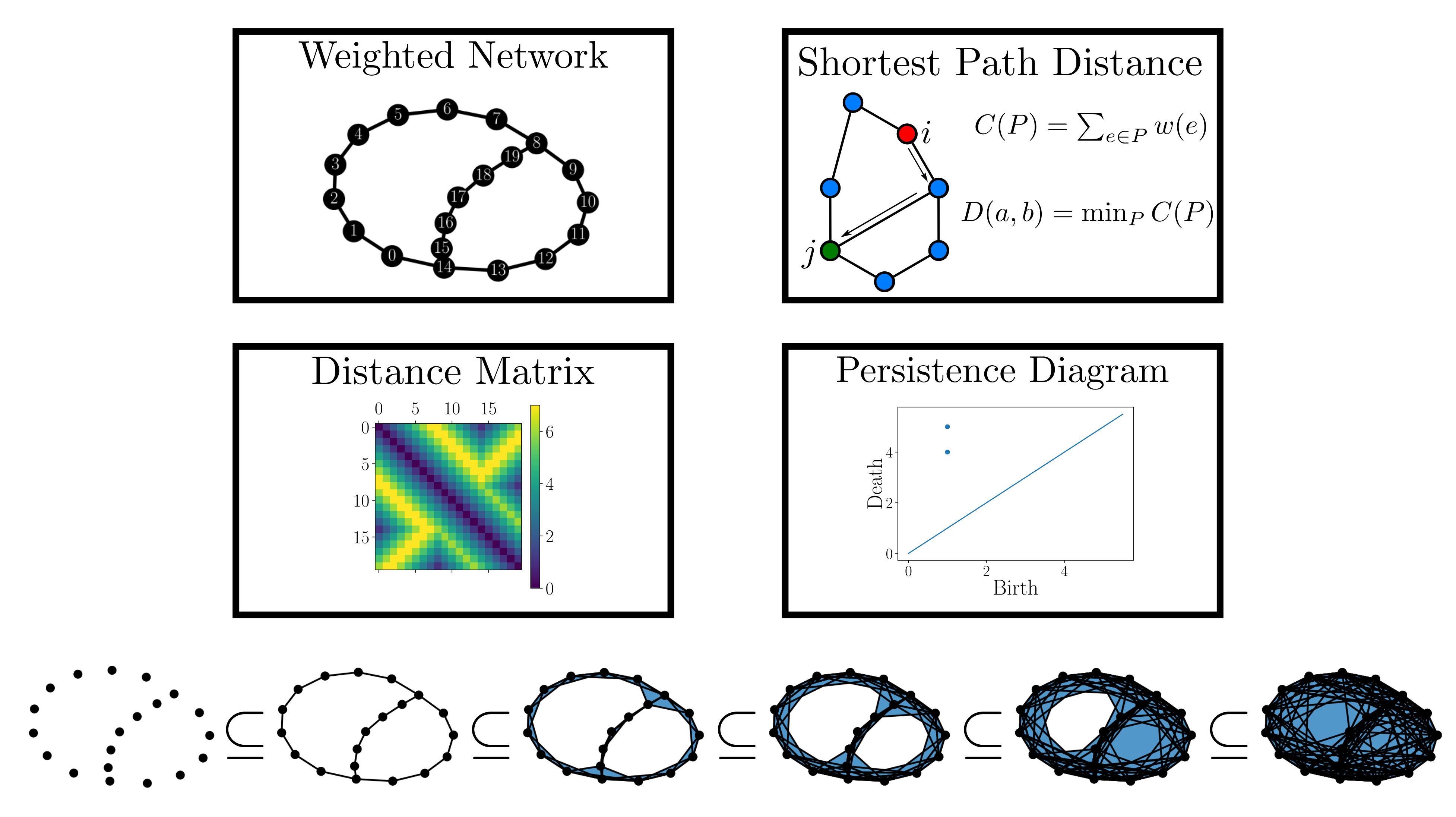 --- # Network Distance Metrics  ??? Other distance metrics can also be used as shown here. These examples show that the distance matrices and corresponding persistence diagrams will be heavily dependent on the metric chosen so it is important to consider multiple notions of distance. --- # Advantages of Persistence 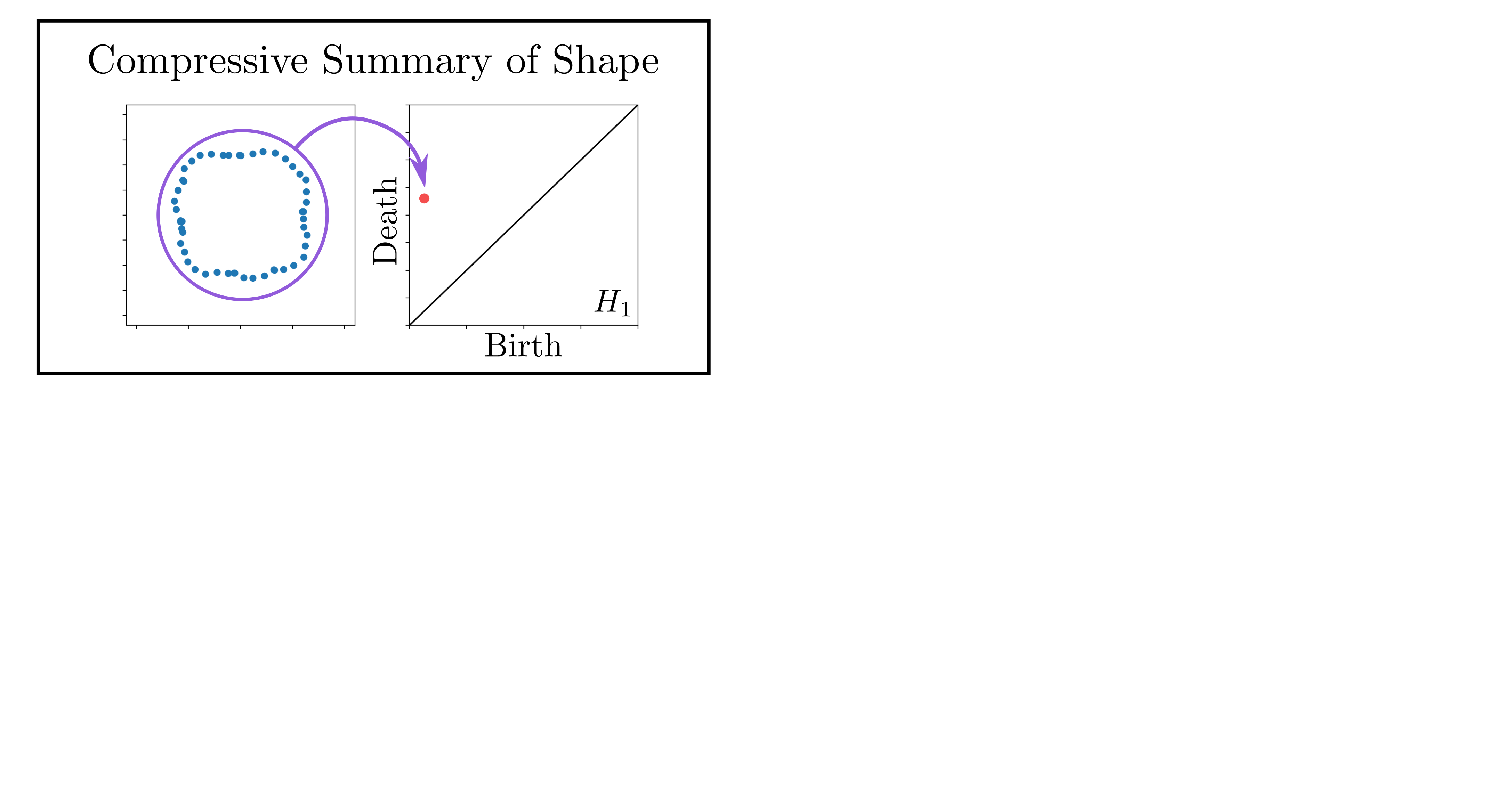 ??? Computing persistent homology has many advantages. It provides a compressive summary of shape for the data by allowing for representing complex structures as a list of few points. It has also been proven that persistence is stable under small perturbations, and is robust to noise where structures due to noise show up near the diagonal. Finally, it is conducive to machine learning allowing for topological features of the data to be integrated into an ML pipeline. --  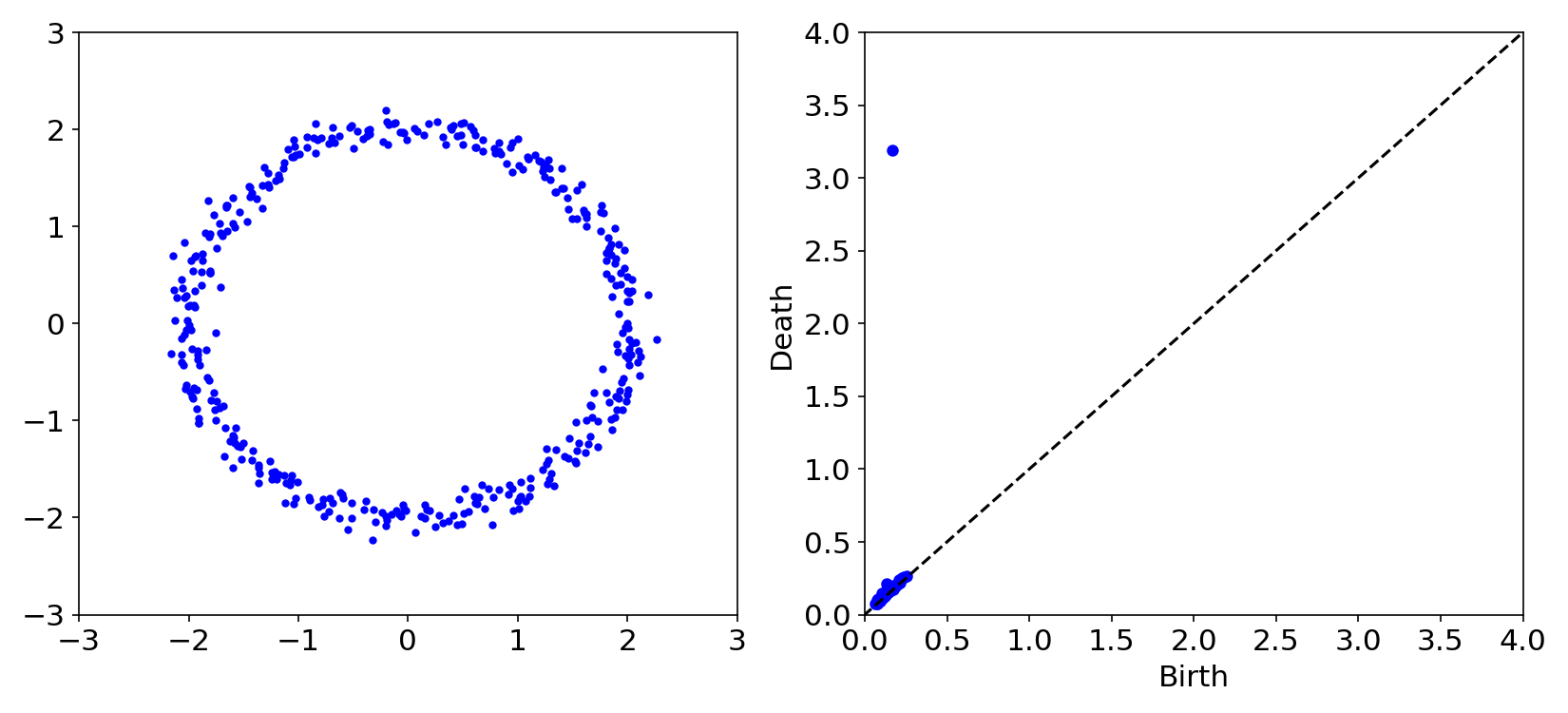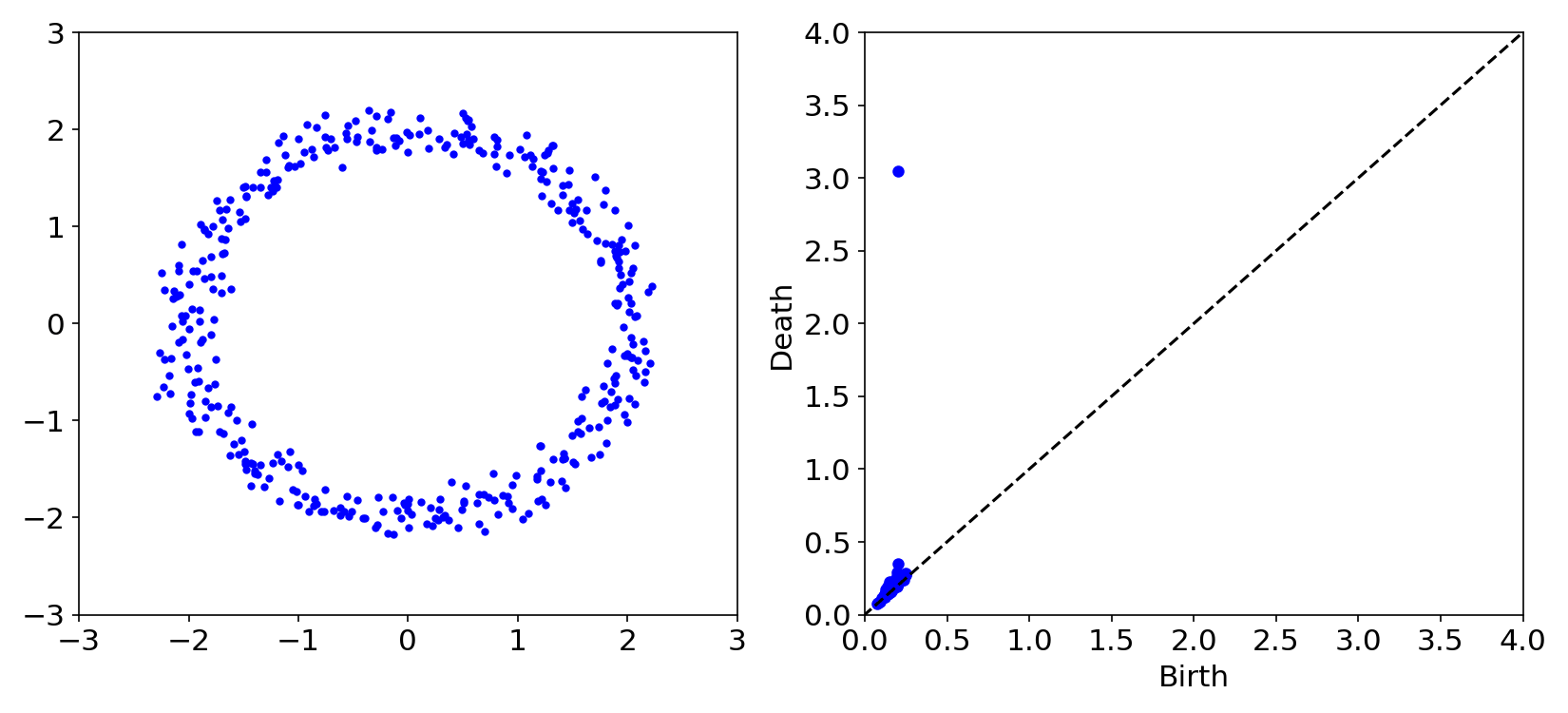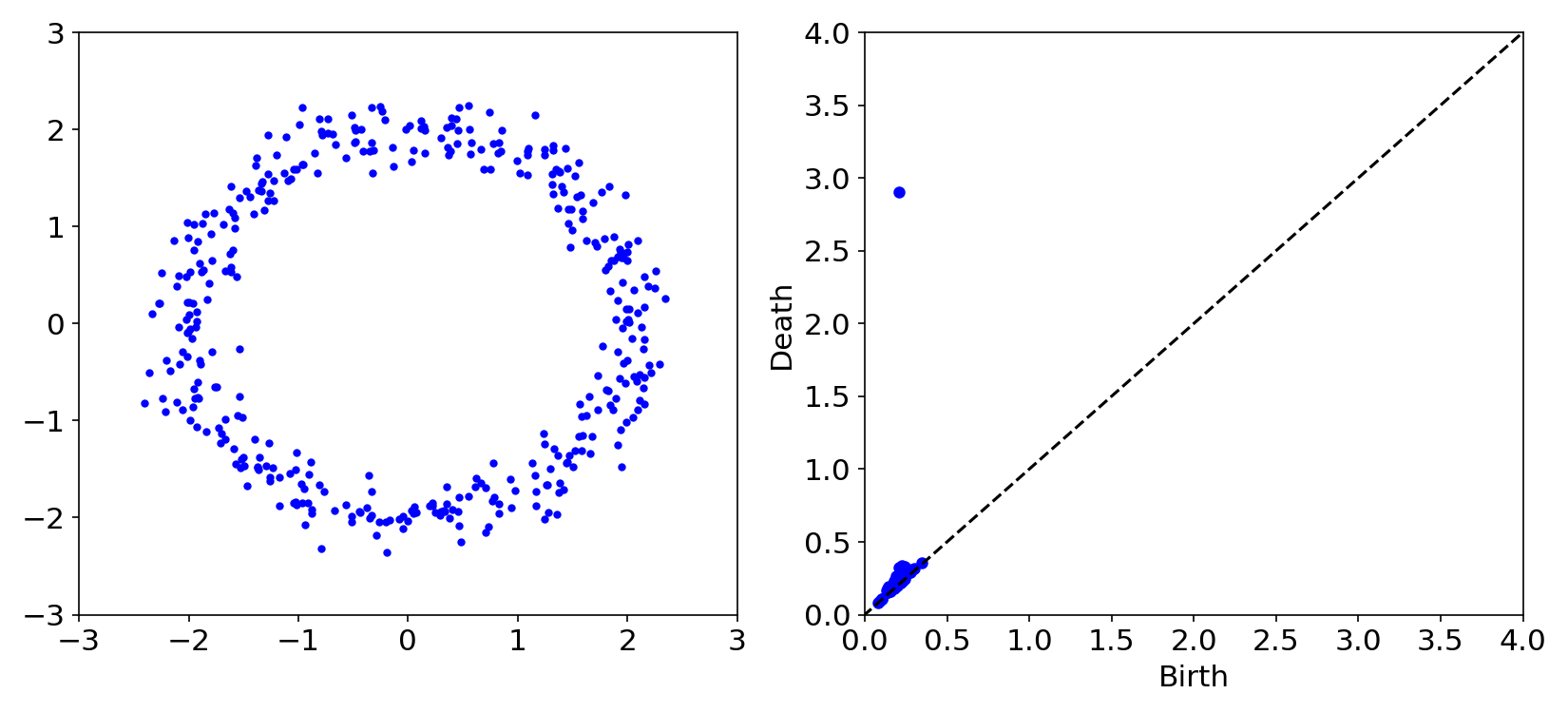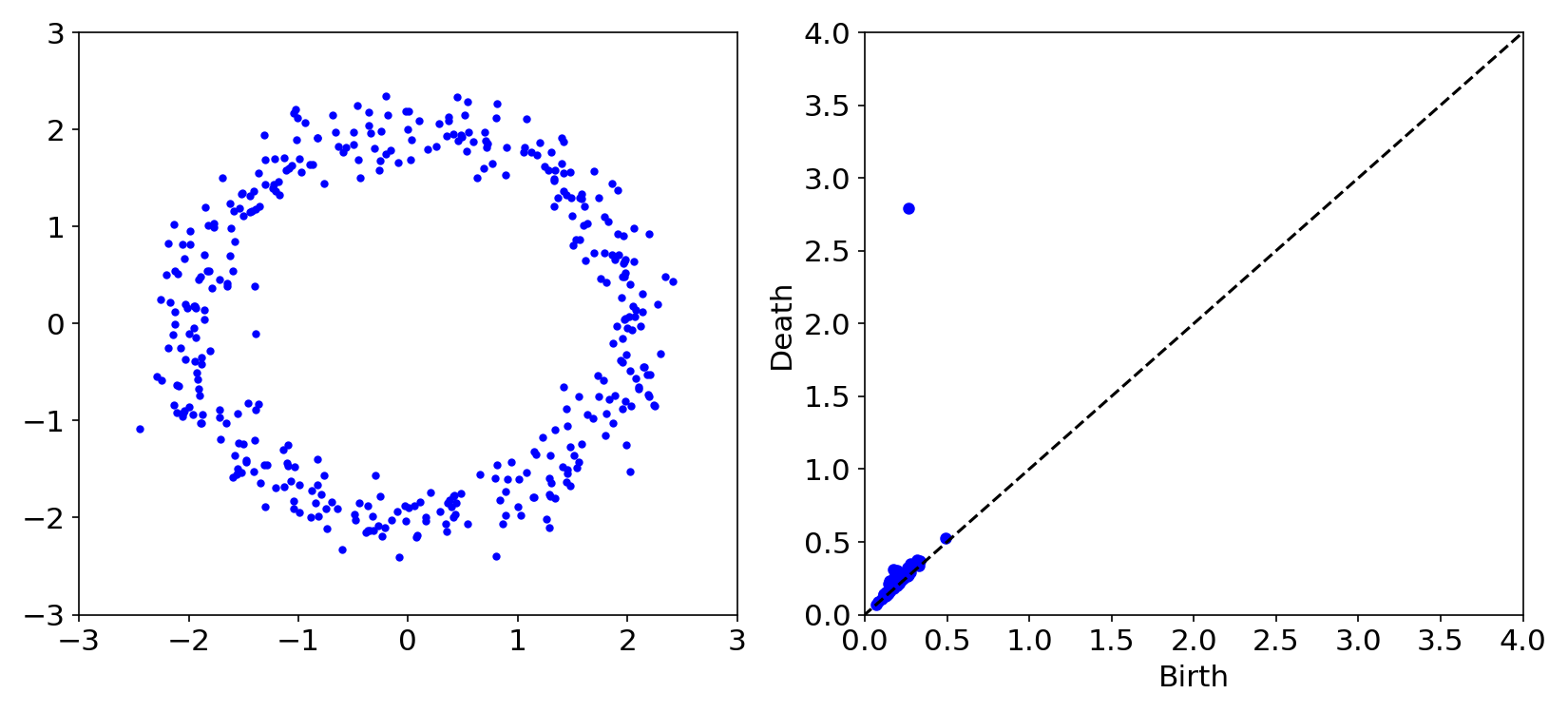 .footnote[ <p style="font-size: 13px;">Cohen-Steiner, et al. "Stability of persistence diagrams." Proceedings of the twenty-first annual symposium on computational geometry. 2005.<br></p> ] -- 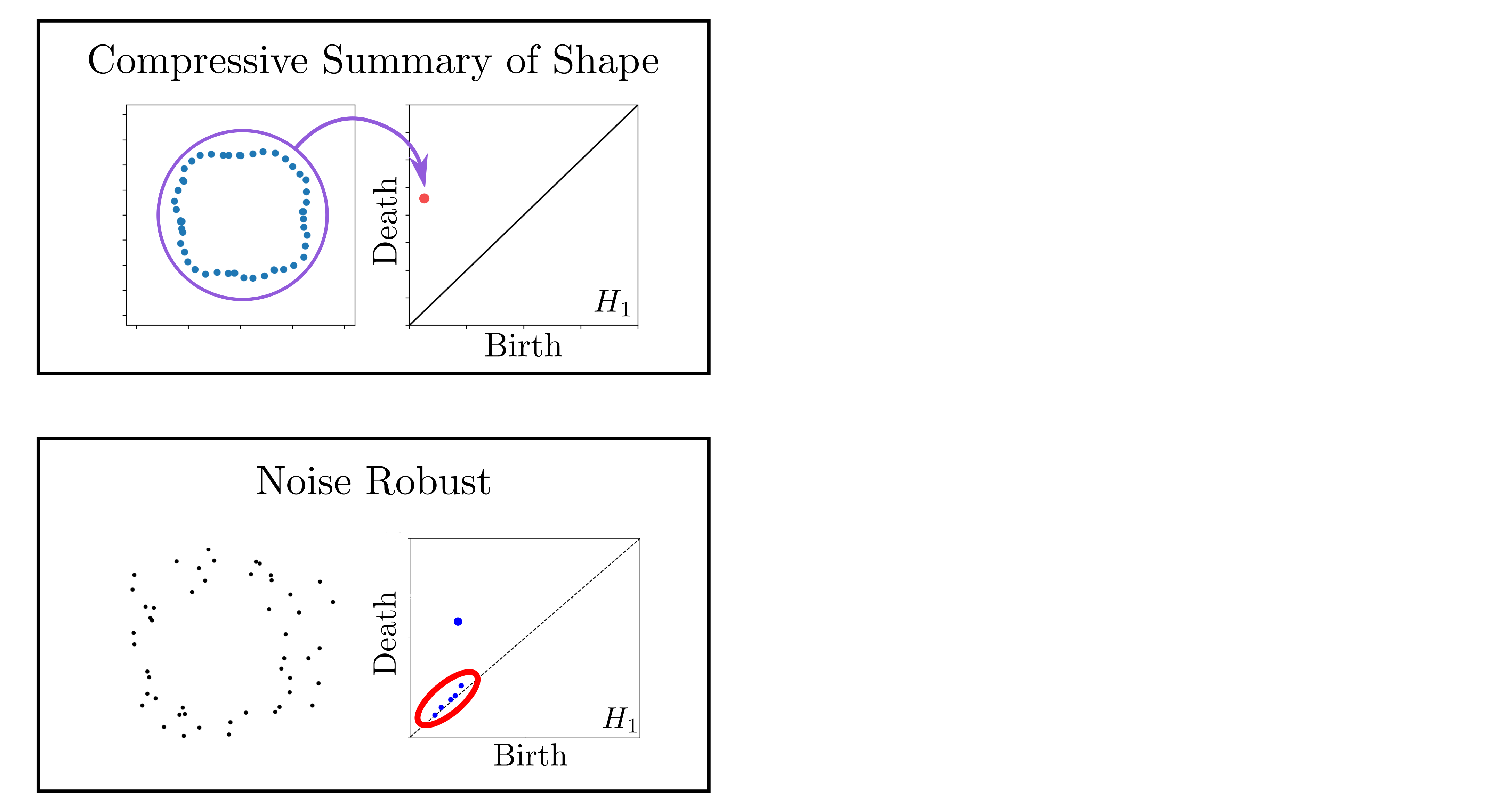 -- 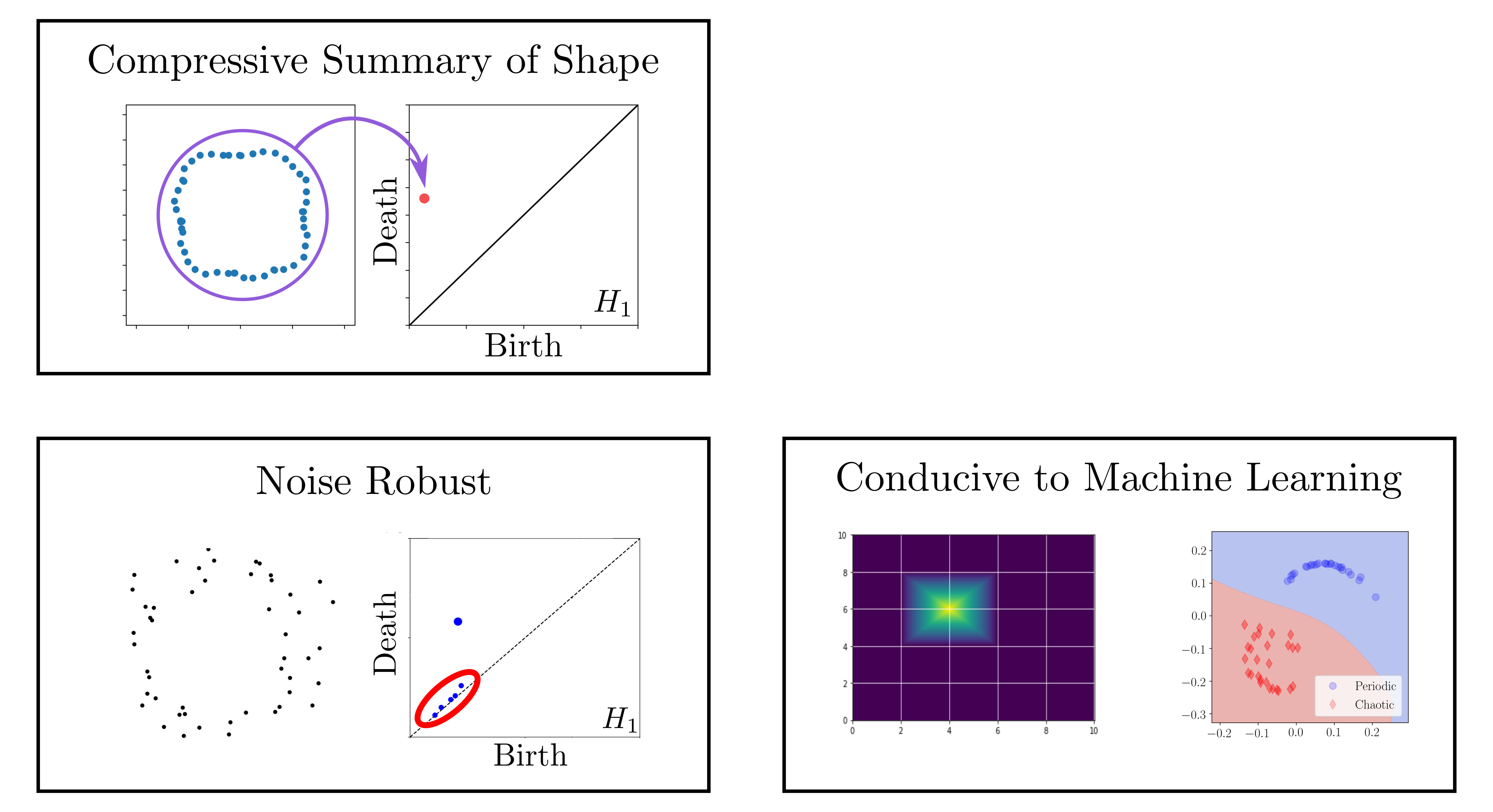 --- # Some Applications of Persistence  ??? Persistence has been successfully applied across many domains such as damping parameter estimation, bifurcation detection, surface texture analysis, chatter detection in machining, quantifying topology of different weather patterns, and stochastic bifurcation detection in dynamical systems. These are only a few of the many other applications of persistence. All of this success has been achieved in the absence of a calculus on the space of persistence diagrams. Recently, a framework for differentiation of persistence diagrams has been introduced that unlocks an entirely new class of problems that can be solved using persistence. --  --  -- 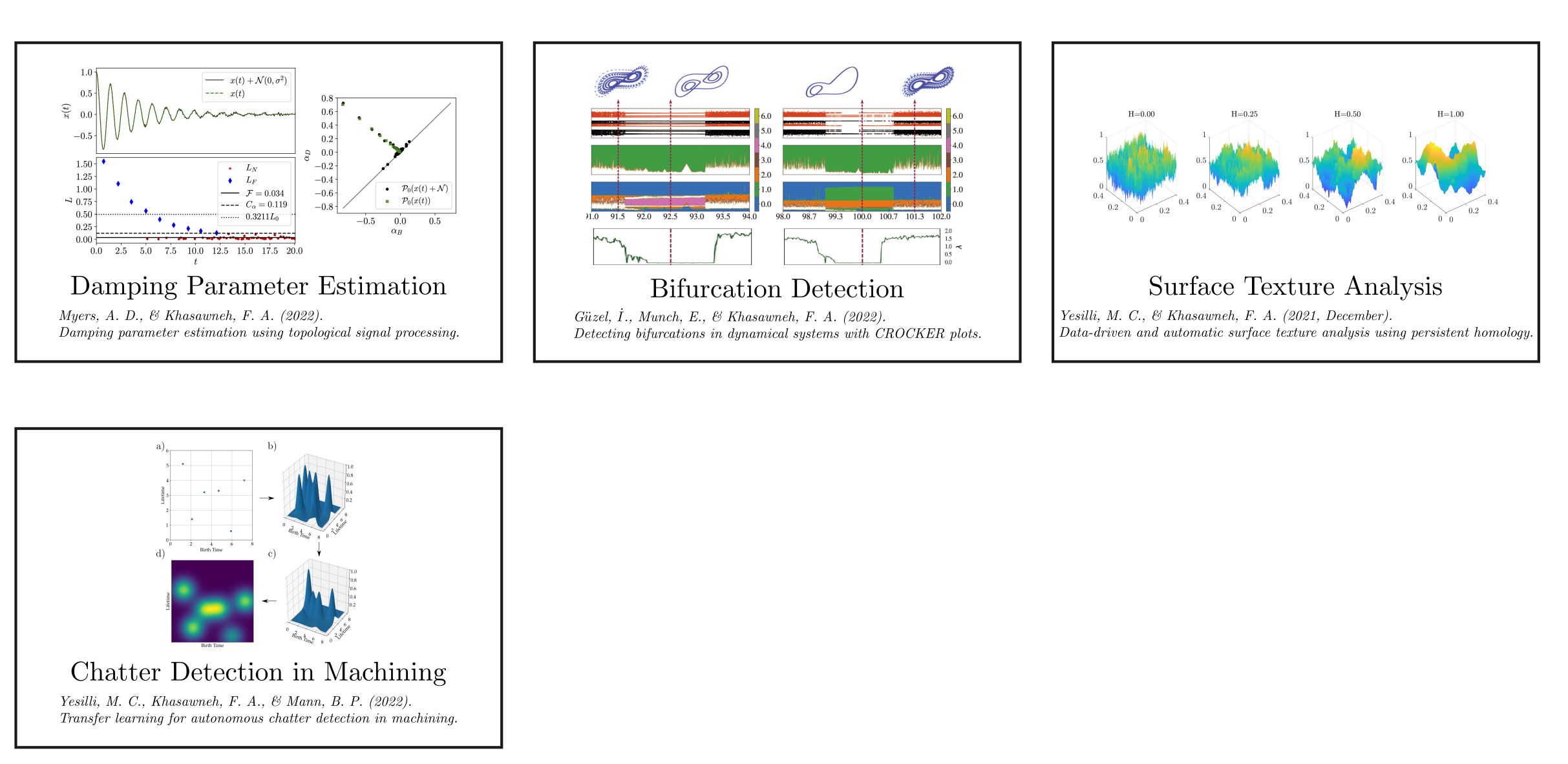 --  -- 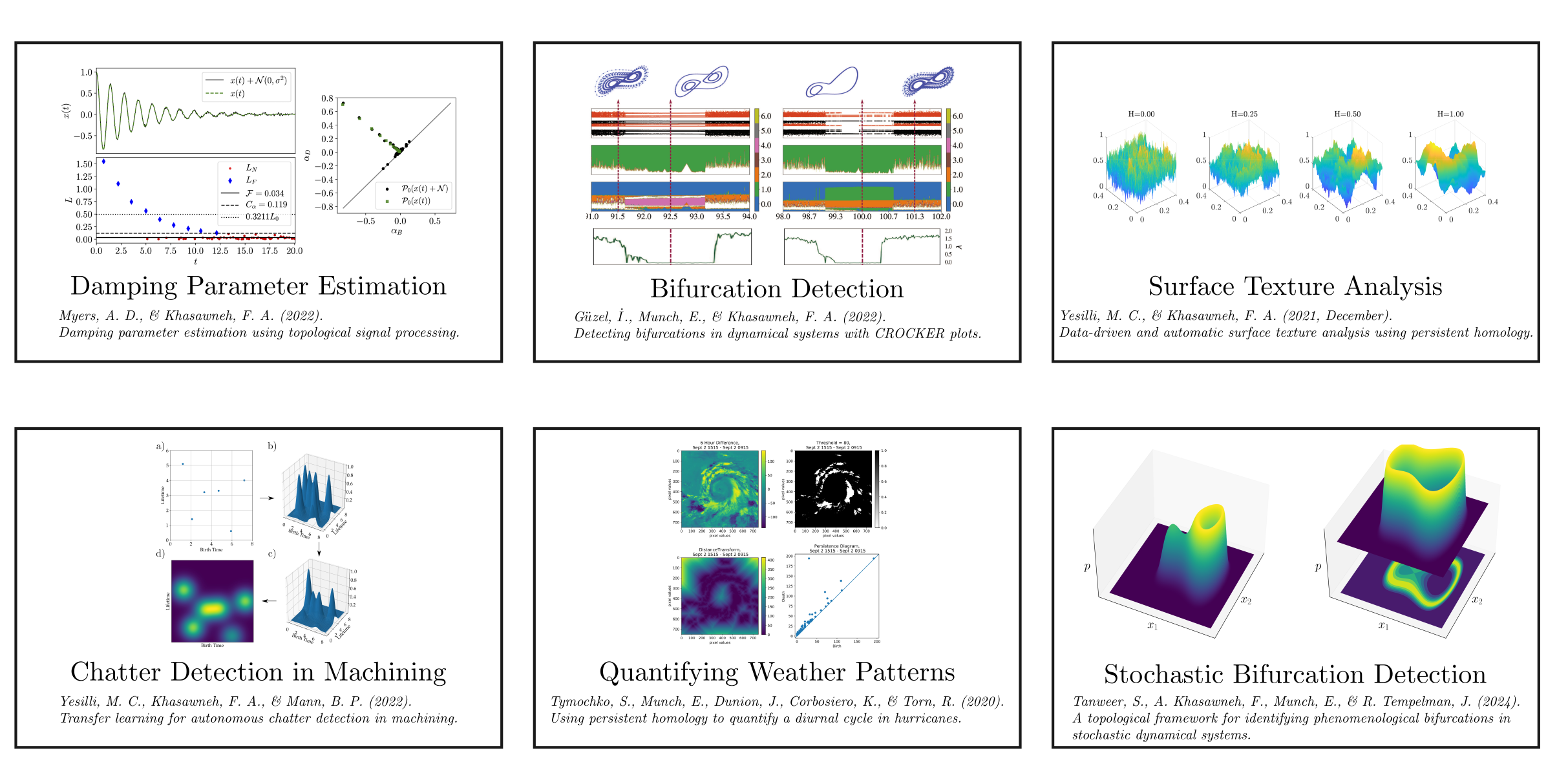 --- # Differentiability of Persistence Diagrams  ??? This leads to my first chapter on persistence optimization. Here I will present the background on how a persistence diagram is differentiated and then propose work for two novel applications of this concept in parameter space navigation for dynamical systems and a new data assimilation framework. --- # Persistence as a Map  ??? To study the idea of differentiability in the space of persistence diagrams it is useful to think of persistence as a map. If I start with a point cloud theta, I can map this point cloud to the persistence diagram using the relevant filter function. For this example I am using the Vietoris Rips filtration. In this case there is one loop that is born at r=b and dies at r=sqrt(2)b. The persistence diagram can then be mapped to a real valued feature with the map V. Here I am showing the total persistence feature which quantifies how far points are from the diagonal. Together, the maps B and V can be composed to form a map composition from point cloud to persistence feature. -- 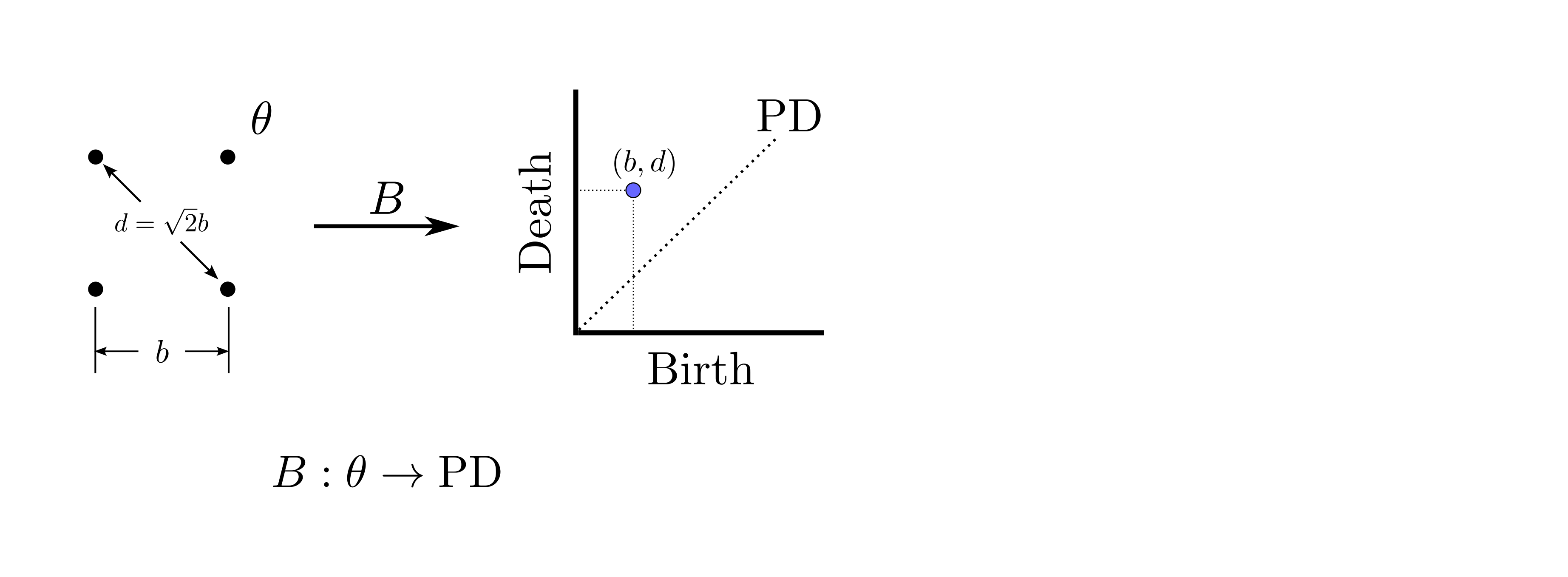 .footnote[ <p style="font-size: 13px;">Leygonie, Jacob, Steve Oudot, and Ulrike Tillmann. "A framework for differential calculus on persistence barcodes." Foundations of Computational Mathematics (2021): 1-63.</p> ] --  --  --- # Functions of Persistence  .footnote[ <p style="font-size: 13px;">Carriere, Mathieu, et al. "Optimizing persistent homology based functions." International conference on machine learning. PMLR, 2021.</p> ] ??? There are many different functions of persistence that can be used to quantify and optimize various topological properties of a point cloud. In order to have differentiability in this pipeline, two criteria need to be satisfied. The function needs to be locally lipschitz and it needs to be definable in an o-minimal structure or in other words definable using finitely many unions of points and intervals. An example of a set that fails this criteria is the cantor set because it requires infinitely many operations to determine if a point is in the set. Most normal functions meet this criteria so we wont have to worry about it too much but it's something to consider when defining new functions of persistence. If both of these conditions are satisfied, the derivative of the map composition V of B is definable. I will now show a few useful examples of persistence functions. First we have the total persistence or the sum of the lifetimes of all persistence features. Maximizing this function would result in a point cloud with large distances between points in 0D persistence or large loops in 1D persistence. The second function of persistence is the maximum persistence which allows for controlling the largest distance between any two points in 0D persistence or the size of the largest loop in the data for 1D persistence. There are also methods for quantifying dissimilarity between two persistence diagrams. The wasserstein distance uses an optimal matching between persistence diagrams to to give a notion of distance between them. This can be used to reach a point cloud that gives a target persistence diagram by minimizing the wasserstein distance. Lastly, persistent entropy gives a measure of order in the persistence diagram and can be used to control the simplicity of a point cloud and when used in combination with other persistence functions can give a simpler solution to the optimization problem. --  --  --  --  --  --- # Differentiability of Persistence Diagrams  ??? Here I will show an example of how a persistence diagram can be differentiated using the Vietoris Rips filtration. I'll start with a simple point cloud of 4 points called theta. We see that this point cloud has a single loop structure if we only consider 1D persistence for now. When the connectivity parameter reaches the value where the loop is born, we call this simplicial complex sigma. At this point, I label the edge that results in the birth of the loop and its vertices as shown. Likewise, we consider the simplicial complex where the loop dies and label those vertices and corresponding edge. Using the map B, we can map theta to a persistence diagram in terms of b and d. This process has been shown previously without labeling the attaching edges in the simplicial complexes. To differentiate this persistence diagram, we consider a perturbation of the point cloud theta called theta prime. In this case I am only perturbing p2 to p2 prime but note that any points can be perturbed. In this case p2 prime is moved along the u hat vector. If we go through the same process of labeling the attaching edges of the corresponding loop in the point cloud we can obtain a persistence map B tilde. We see that the attaching edge b prime is now smaller than b and d prime remains equivalent to d. In the persistence diagram this corresponds to the persistence pair moving to the left. Thus the derivative of the persistence map B with respect to the perturbation persistence map B tilde is the unit vector pointing to the left. More generally, using the rips filtration the derivative of the persistence map is computed as a set of vectors (one for each persistence pair) with components consisting of inner products of the distances between vertices at the end points of attaching edges and the unit vector perturbations of the points. This can be further generalized to include infinite persistence pairs and for other filter functions, but I will only consider the rips filtration for now. --  --  --  --  --  --  --  --  --  --  .footnote[Leygonie, Jacob, Steve Oudot, and Ulrike Tillmann. "A framework for differential calculus on persistence barcodes." Foundations of Computational Mathematics (2021): 1-63.] --- # Differentiability Example 1 - 0D Persistence  ??? Here I will show another example of this process using 0D persistence. If I start with the point cloud shown, we see that the persistence diagram consists of a single connected component. If we consider the space of small perturbations of this point cloud or a lift into a higher dimensional space we can map this space of perturbations onto the perturbed persistence diagram. The quotient of this map collapses to the original persistence diagram. For the specific perturbation shown here we see that the distance between the points increases so the derivative in this case is a vector in the vertical direction and if we want to maximize the change in the persistence pair, the perturbation vectors should be in opposite directions. In other words the distance vector and perturbation vector should be parallel. -- 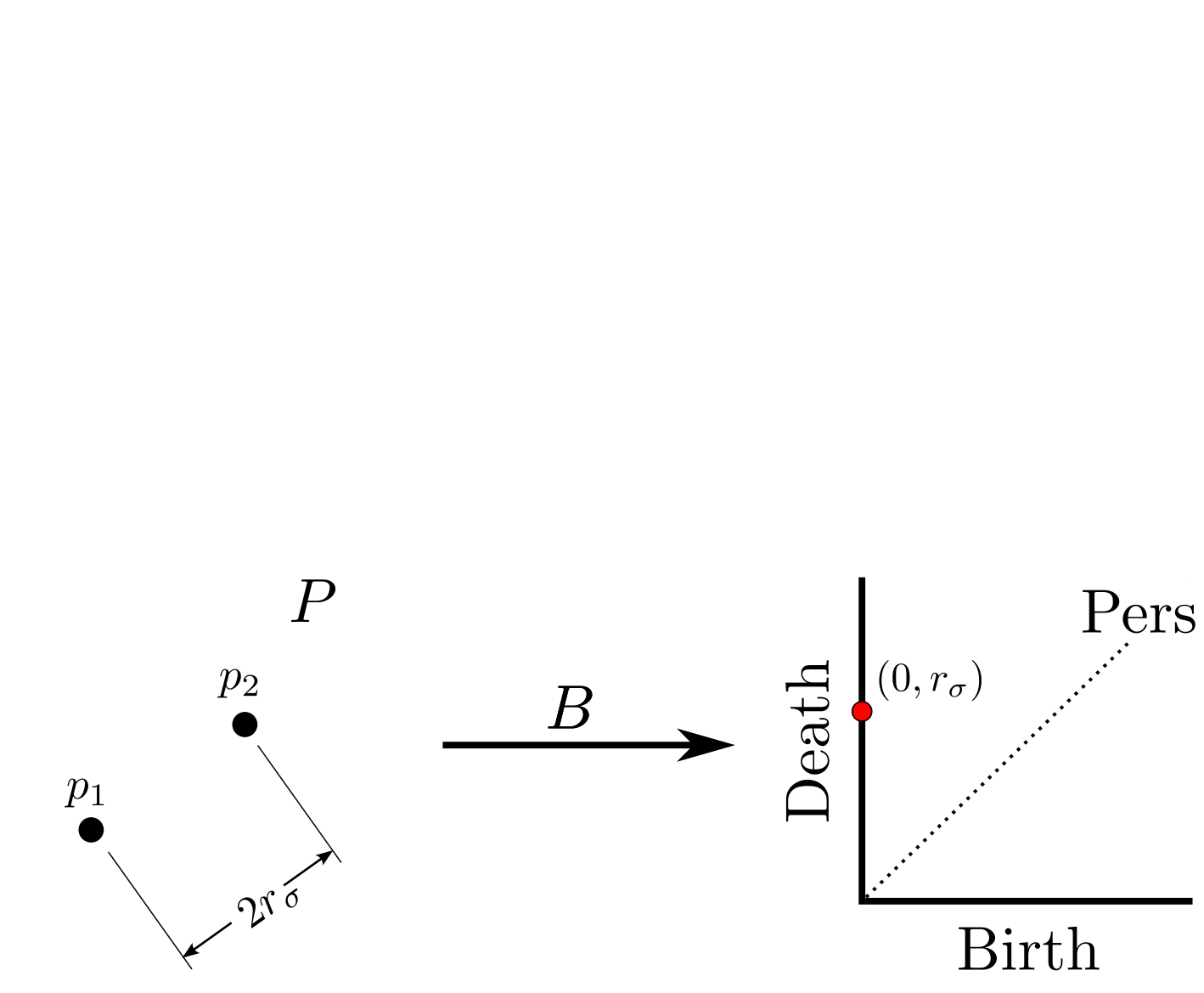 -- 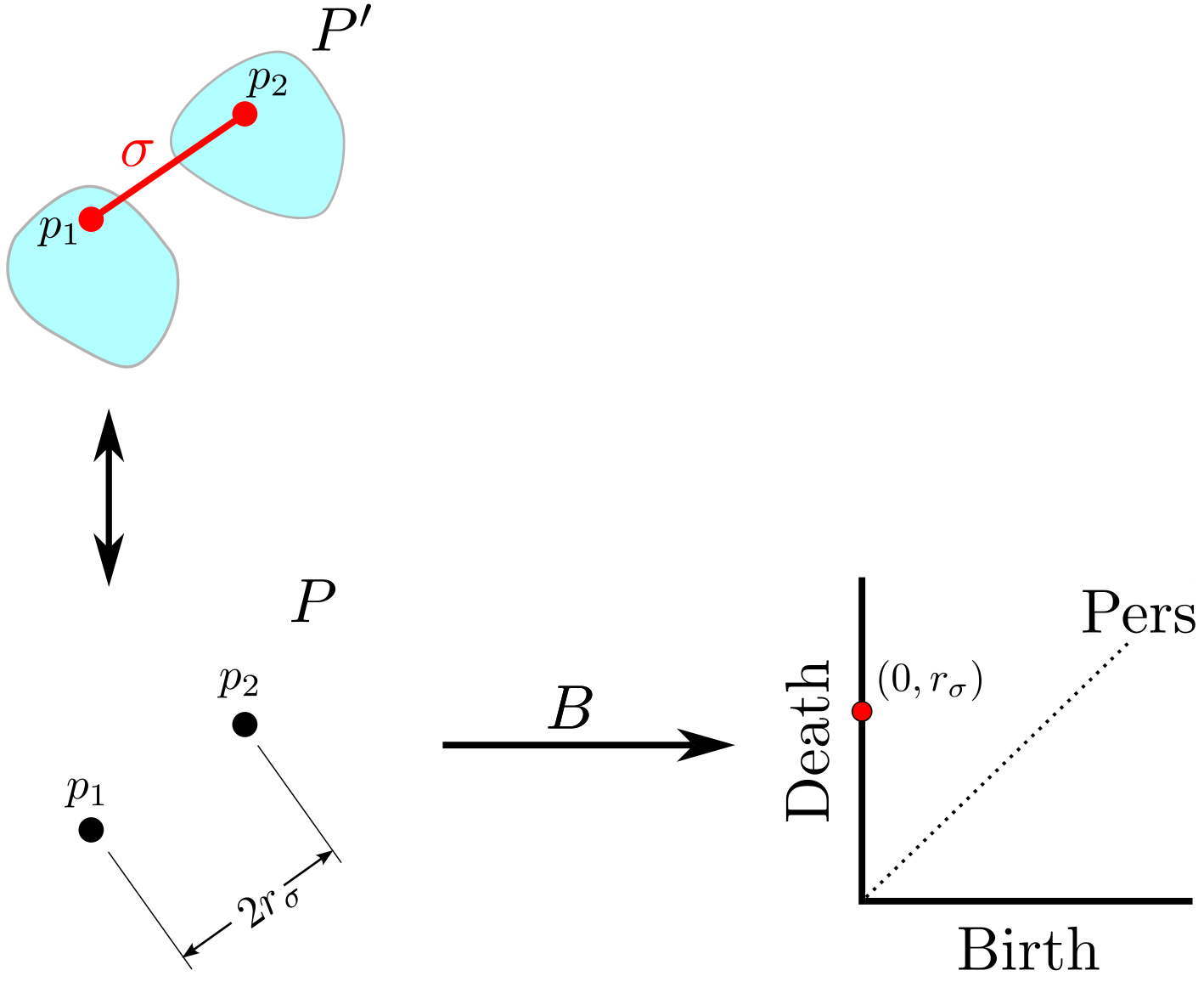 -- 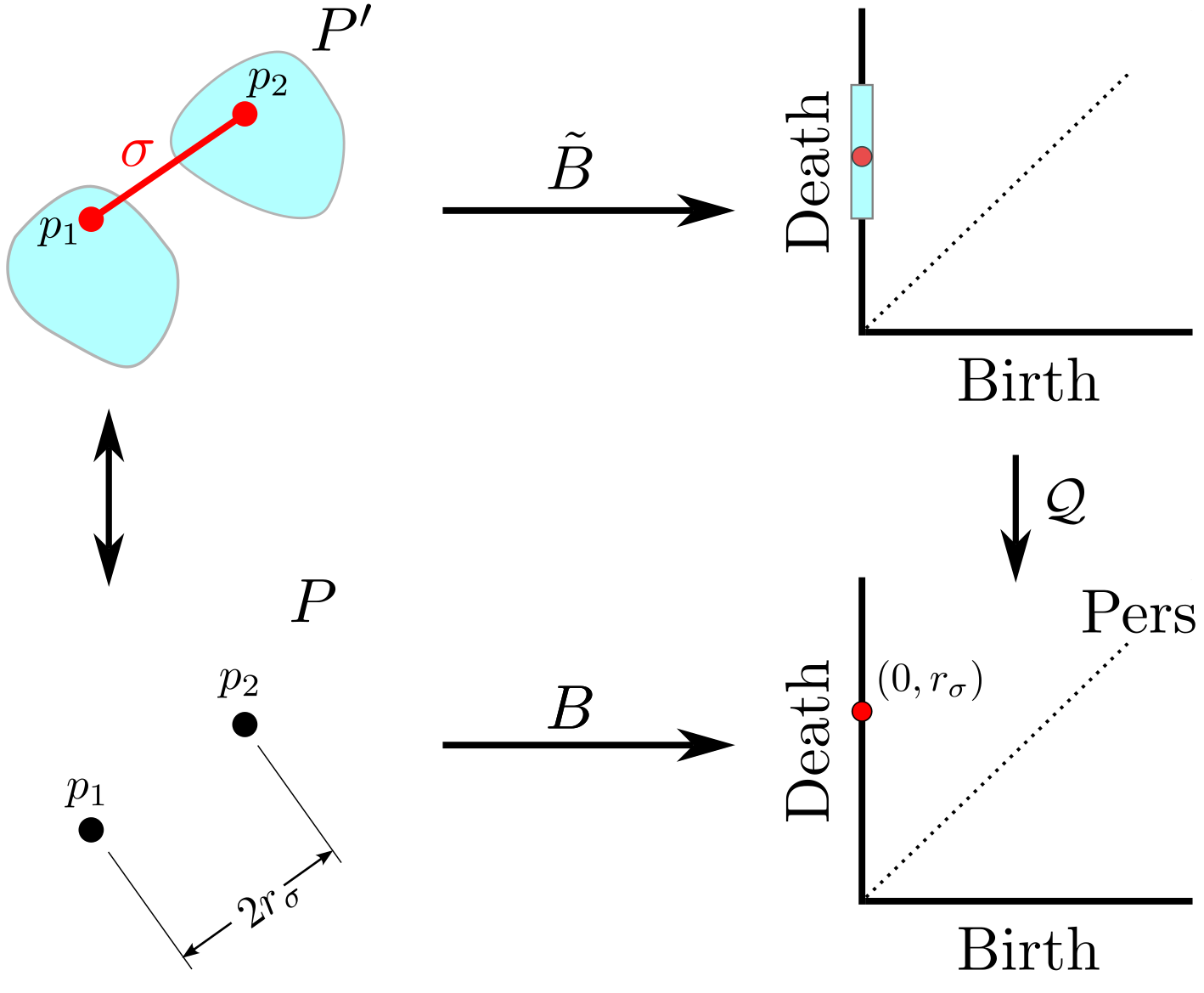 -- 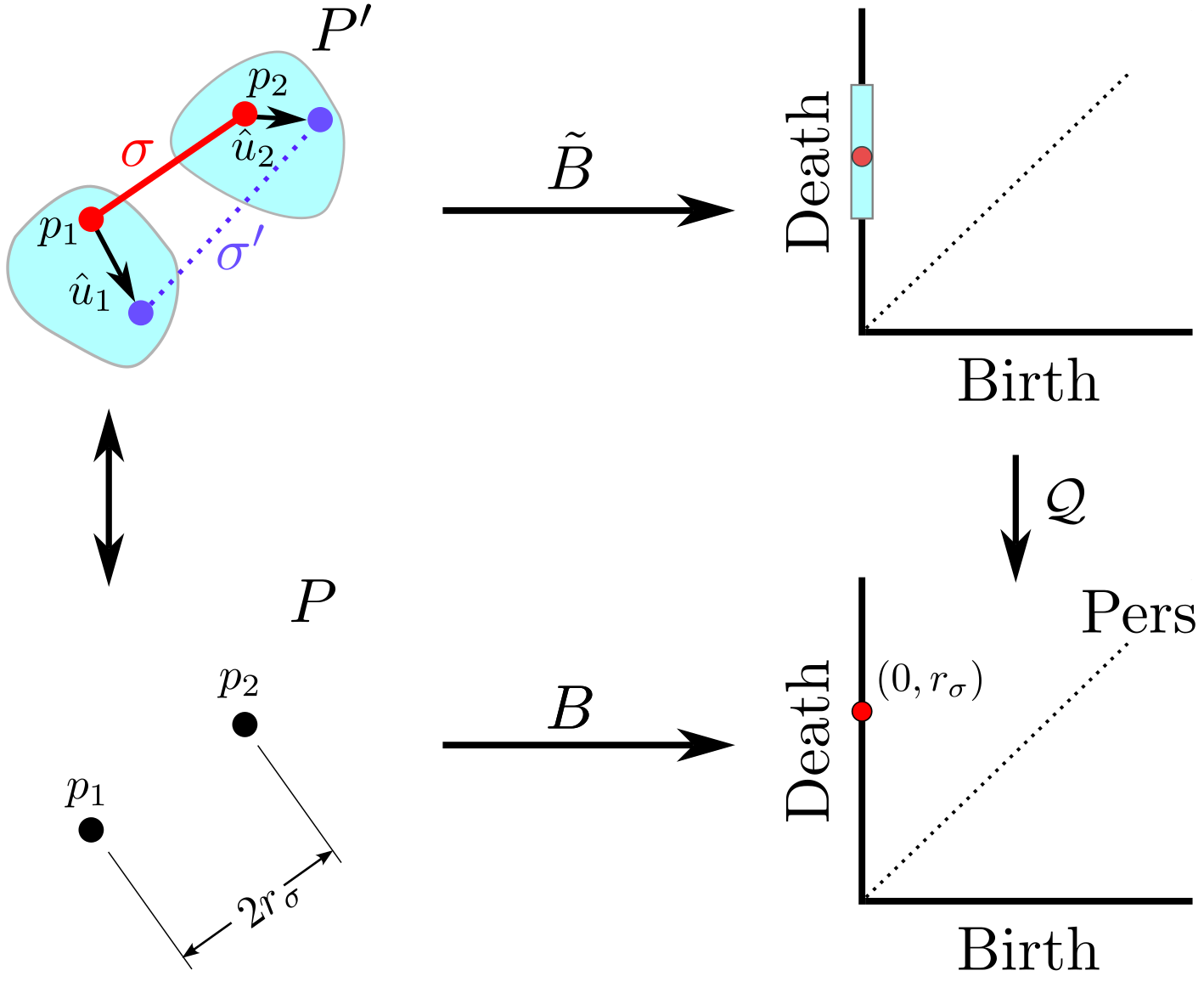 -- 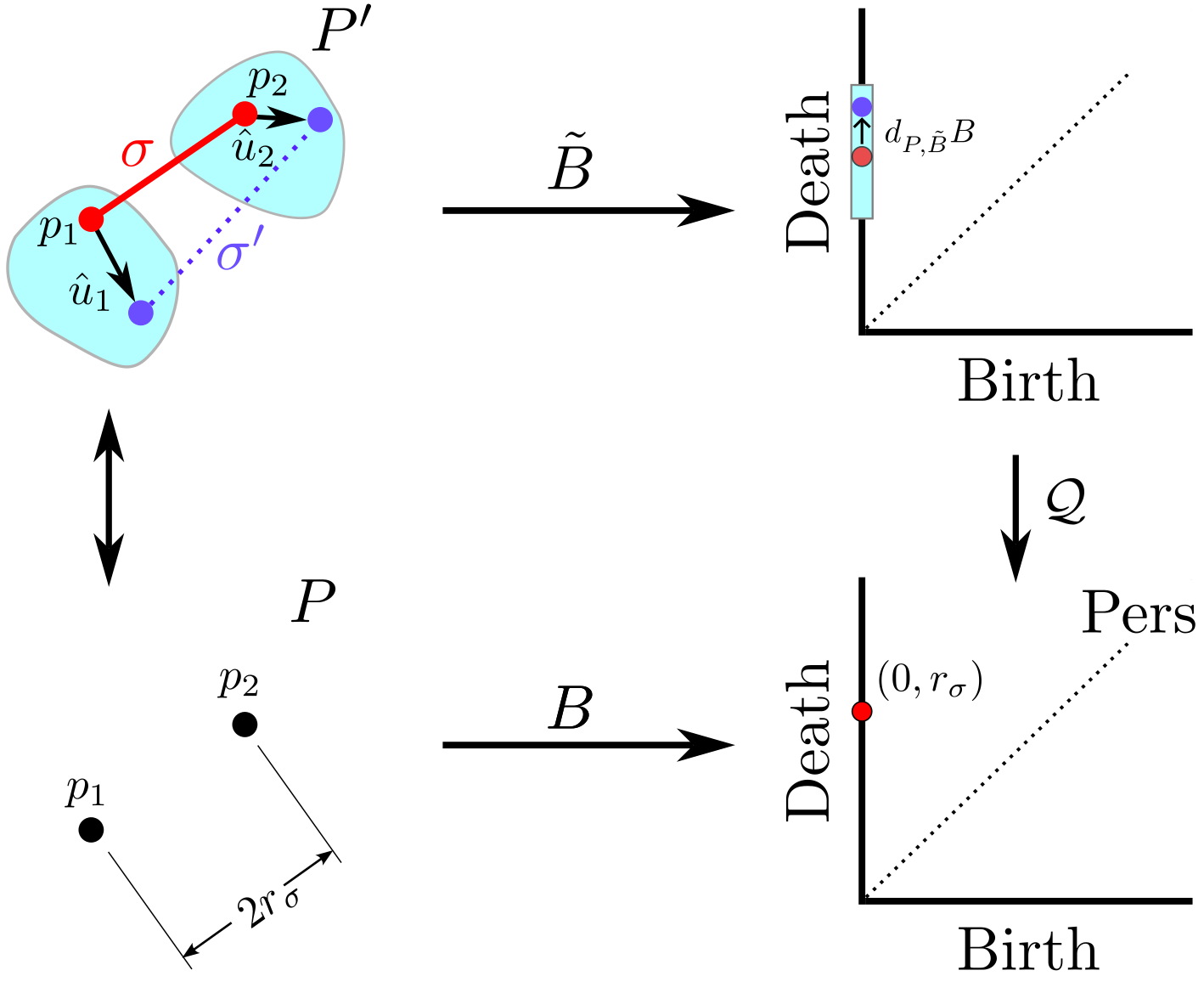 --- # Differentiability Example 2 - 1D Persistence  ??? For the last example, I will go through the process again for a 1D persistence case with a square point cloud to demonstrate the restrictions of this method. For this point cloud, the loop is born at r=b and dies at r=sqrt(2)b and this is reflected in the persistence diagram. If I perturb this point cloud by moving all points in the outward direction by increasing the birth time to b+epsilon we see that the resulting birth and death times increase and the corresponding derivative of this persistence pair in this case is parallel to the diagonal. Now if I choose a different perturbation by only expanding the point cloud in the horizontal direction, we see that the derivative is equivalent to the other case. This shows that to obtain a specific change in the persistence diagram, the perturbation of the point cloud may not be unique which can cause issues for solving this inverse problem. -- 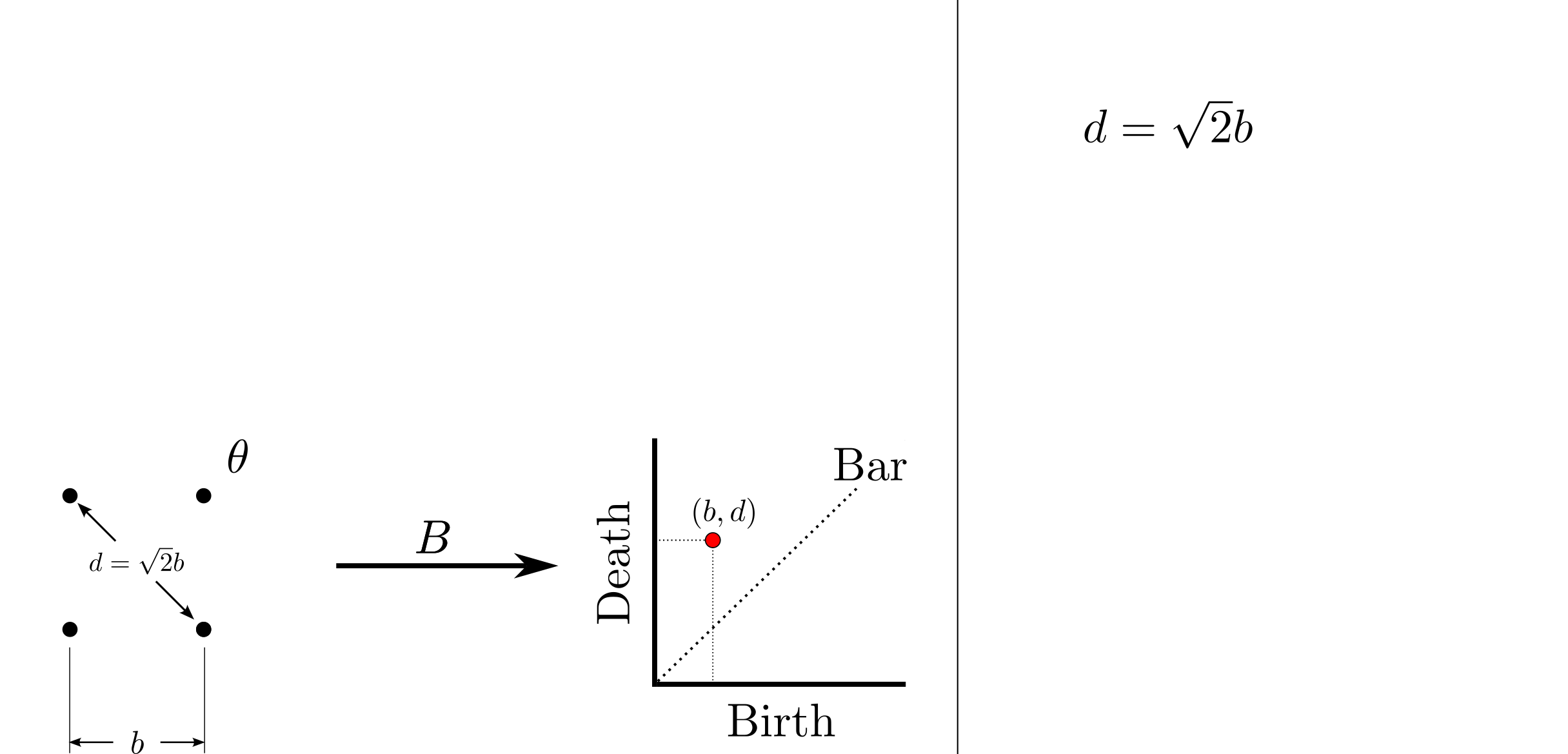 -- 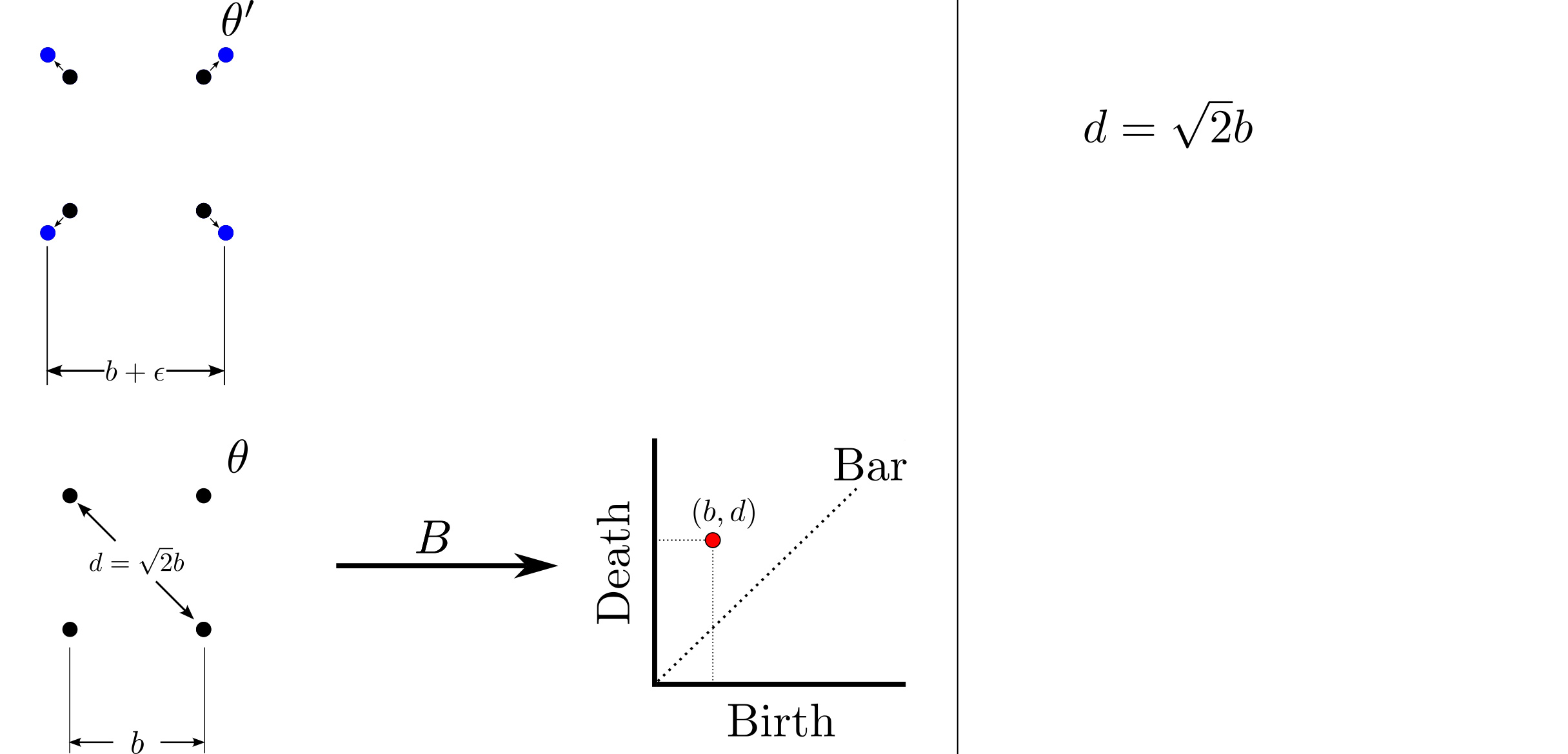 -- 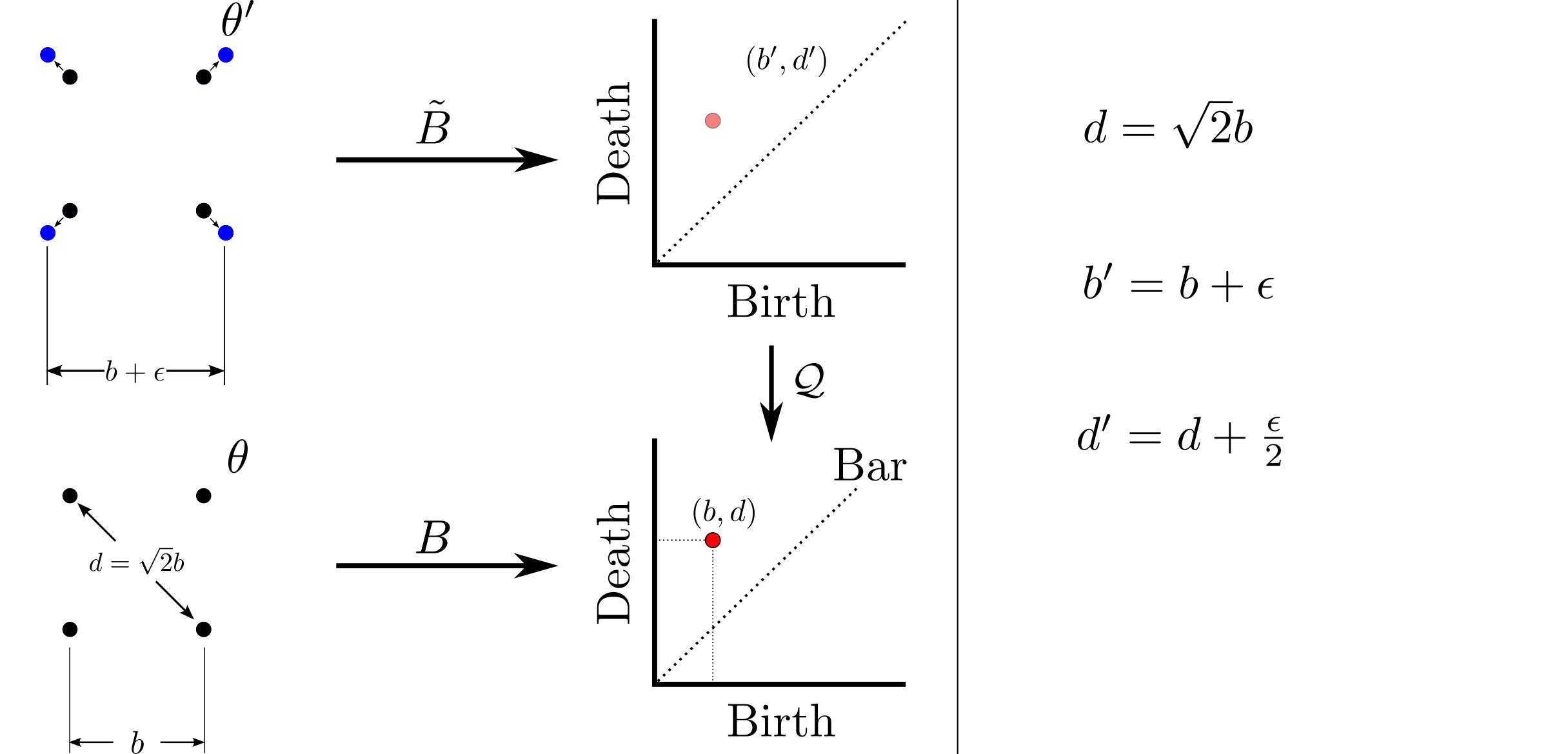 -- 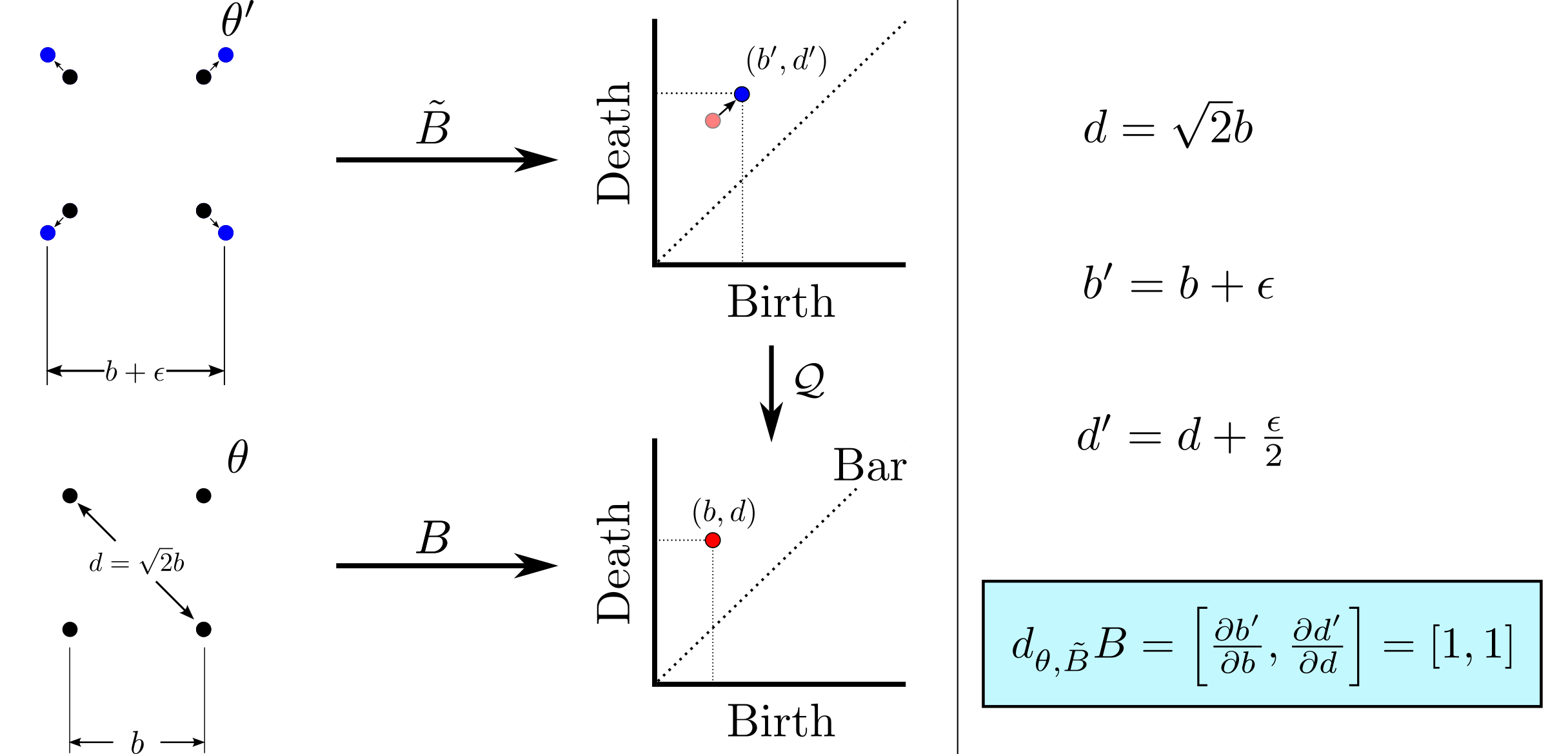 -- 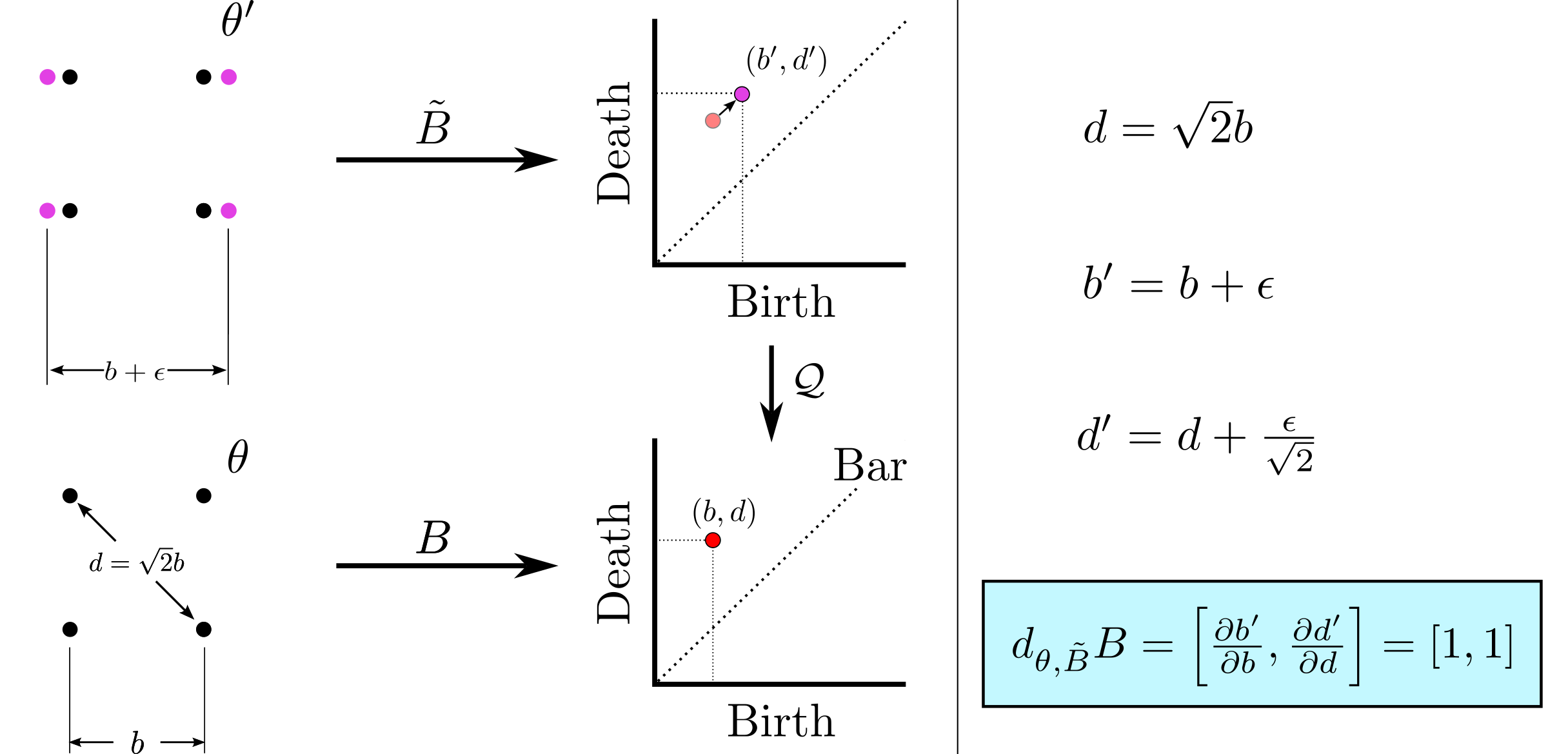 --- # General Position Criteria - `\(\forall i\neq j\in\{1,...,n\},~p_i\neq p_j\)` 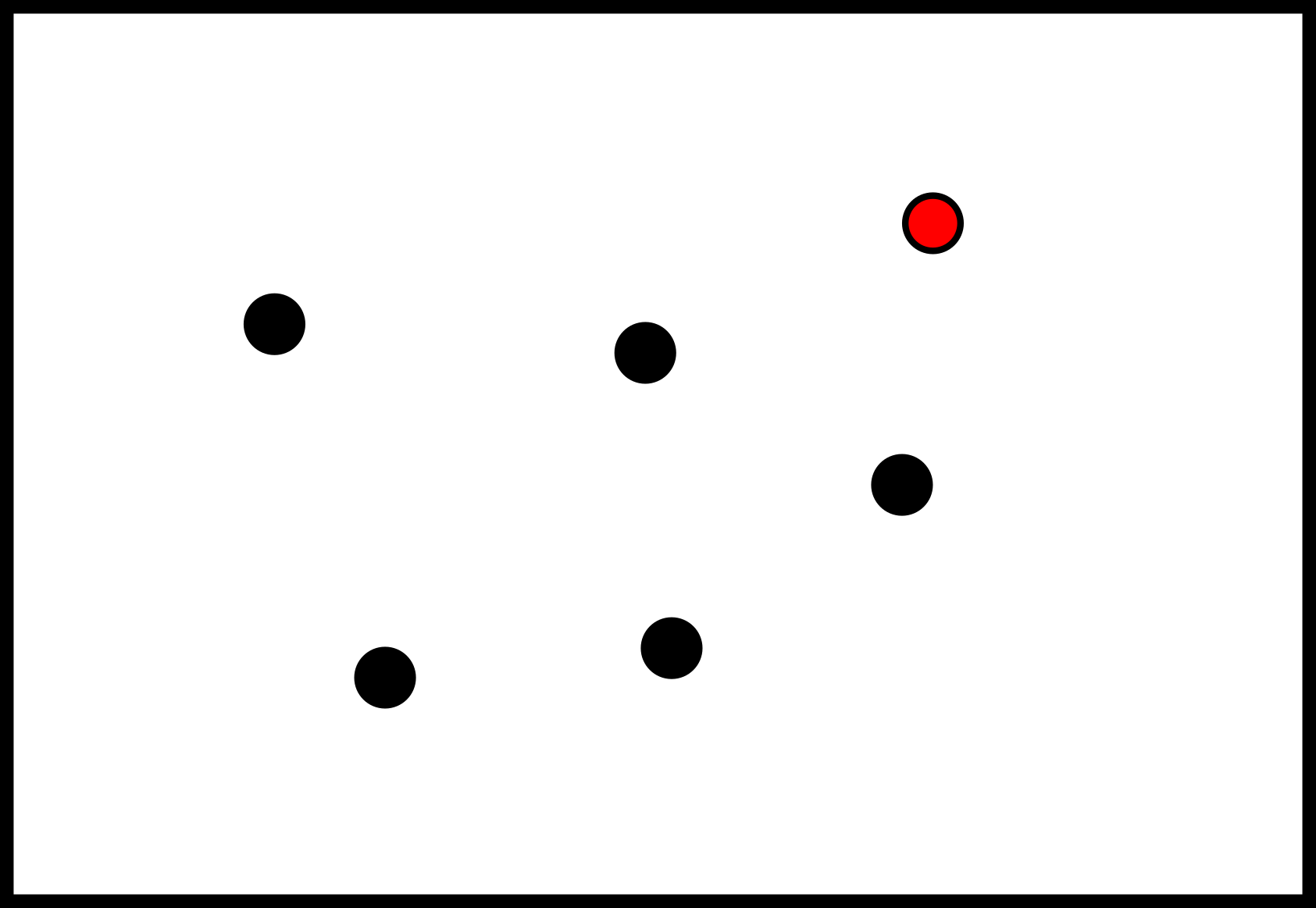 .footnote[Leygonie, Jacob, Steve Oudot, and Ulrike Tillmann. "A framework for differential calculus on persistence barcodes." Foundations of Computational Mathematics (2021): 1-63.] ??? To avoid this issue, conditions need to be defined that guarantee a unique perturbation. For the rips filter function, it has been shown that the point cloud must be in a so called general position. This means that no two points are in the same position. and no two pairs of points are equidistant. At first this can seem like a very limiting constraint on the method, however all this means is that the perturbation may not be unique for a given derivative. In a computational setting it is unlikely that either of these constraints will be violated due to floating point precision and if they are violated the optimization scheme will choose a perturbation and continue the process. Artificial noise can also be introduced if two points are in the same location to avoid a division by zero but again this is highly unlikely for real data. -- - `\(\forall \{i,j\}\neq\{k,l\},~i,j,k,l\in\{1,...,n\},~||p_i-p_j||_2\neq||p_k-p_l||_2\)` 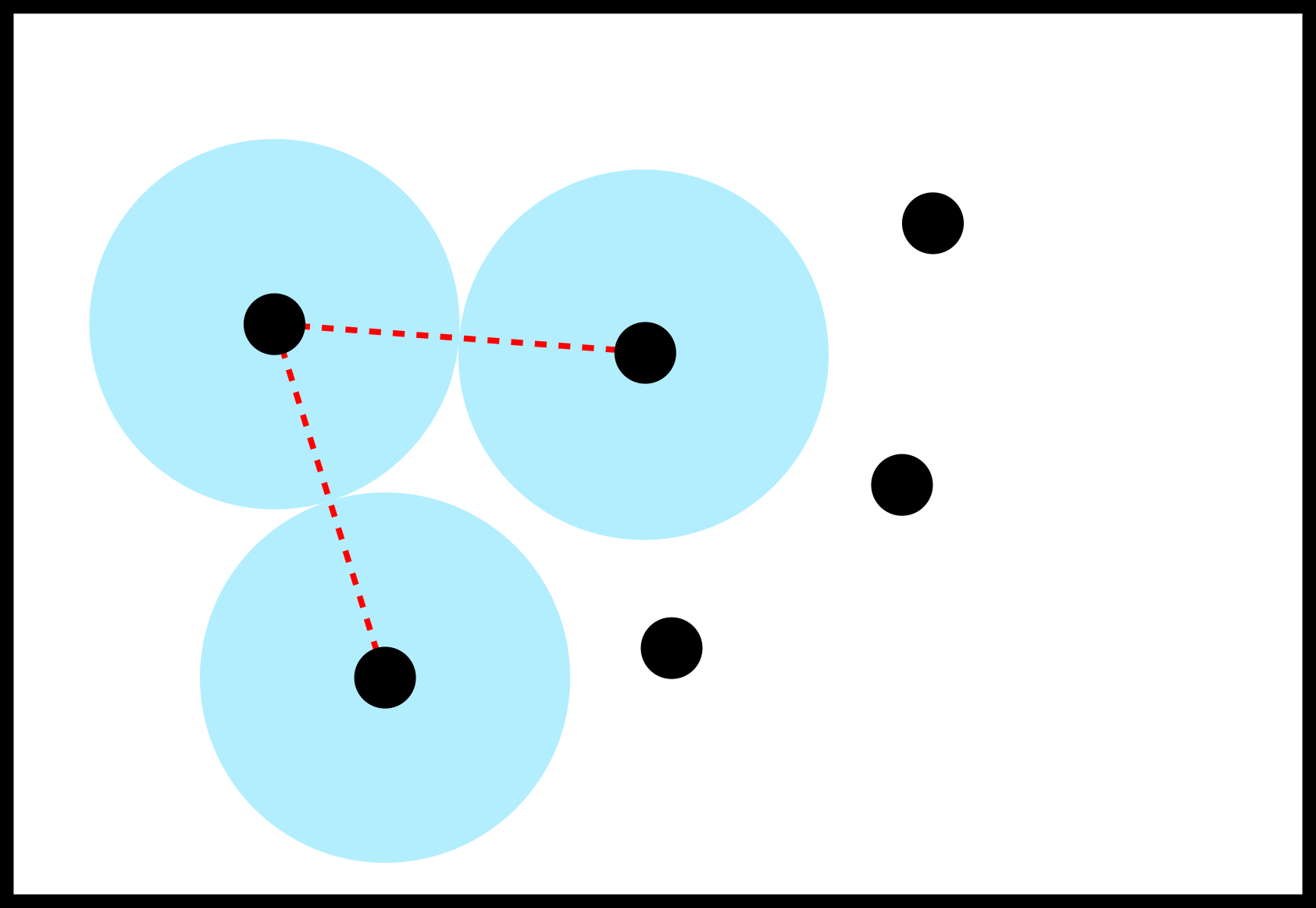 --- # Persistence Optimization 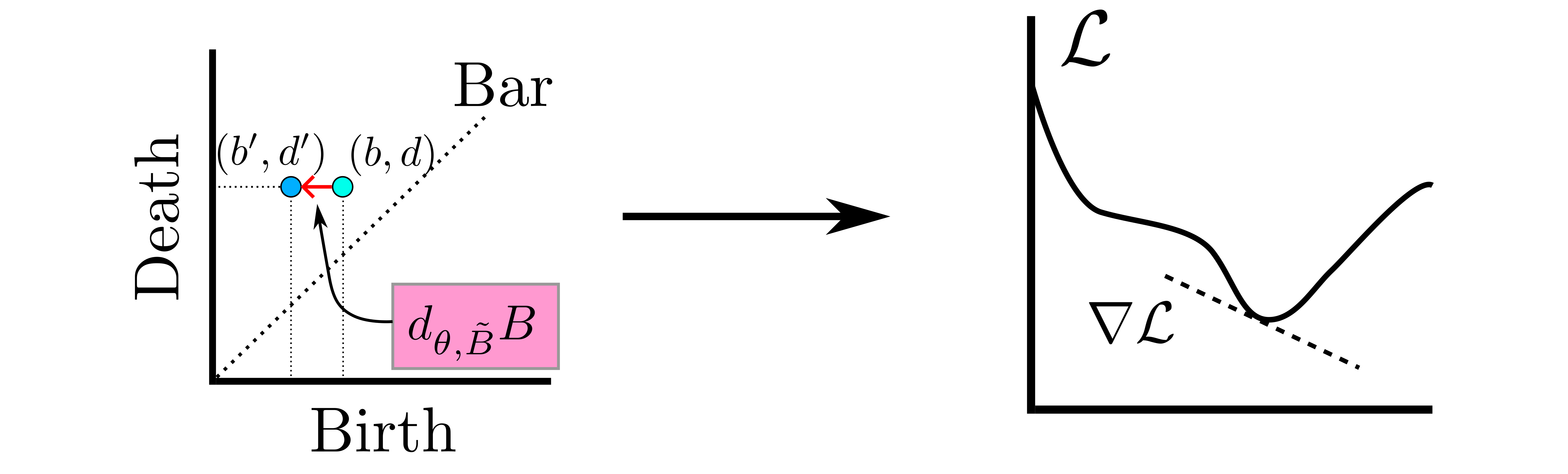 ??? Now that I have defined what it means to differentiate a persistence diagram, I can define a cost function to promote desired topological properties of a point cloud by controlling features of the persistence diagram. The ability to differentiate functions of persistence enables gradient descent optimization to reach a point cloud that minimizes the cost function. Tensorflow and the gudhi python library can be used to perform this gradient descent operation on persistence diagrams. For the first example I defined a cost function using two terms. The first term is the opposite of the total persistence so by minimizing L we are promoting larger loops in the point cloud and 1D persistence diagram. The second term is a regularization term to promote points remaining within a 2x2 square of space. If I start with a circular point cloud with some additive noise, performing the optimization results in a point cloud consisting of a large loop and we see that the persistence pair moves in the vertical direction. Based on how the cost function was defined the minimum is clearly nonzero but due to the regularization term it reaches a minimum of approximately -3 after about 2000 gradient descent steps. The minimizer can be reached faster by changing the learning rate scheduler settings, but for now all that matters is that a solution is achieved. -- 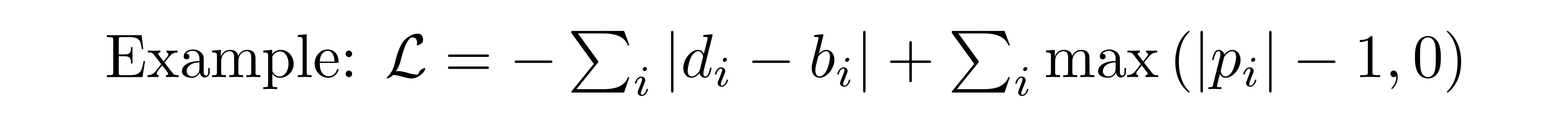 -- 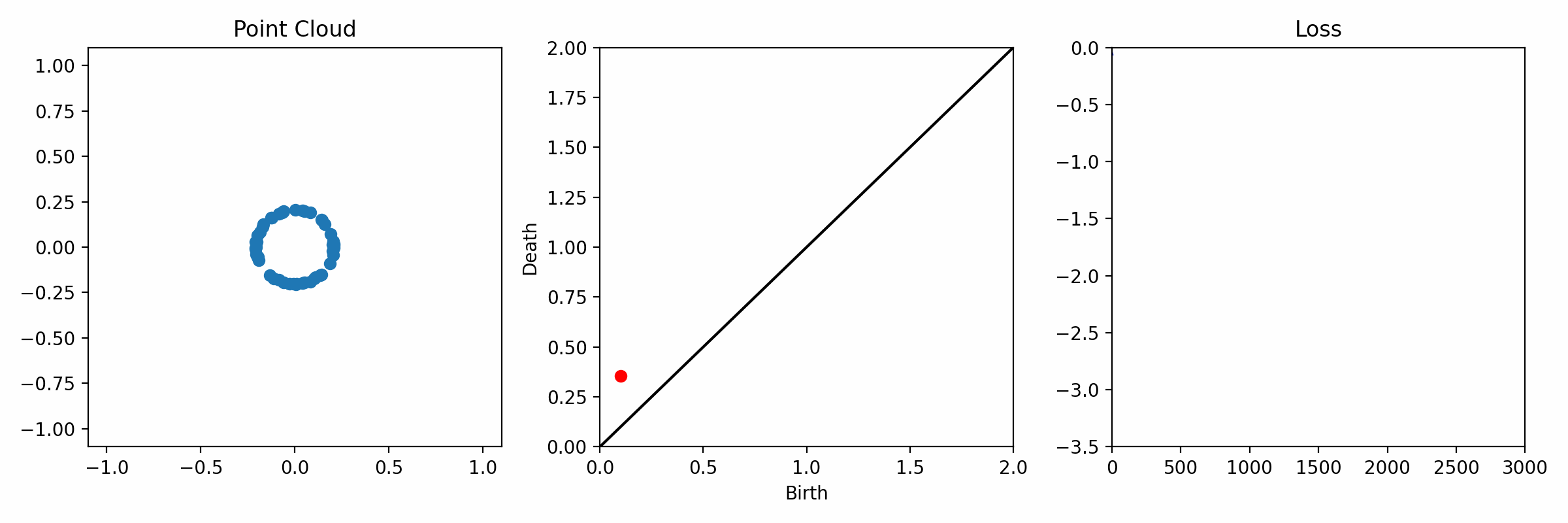 -- 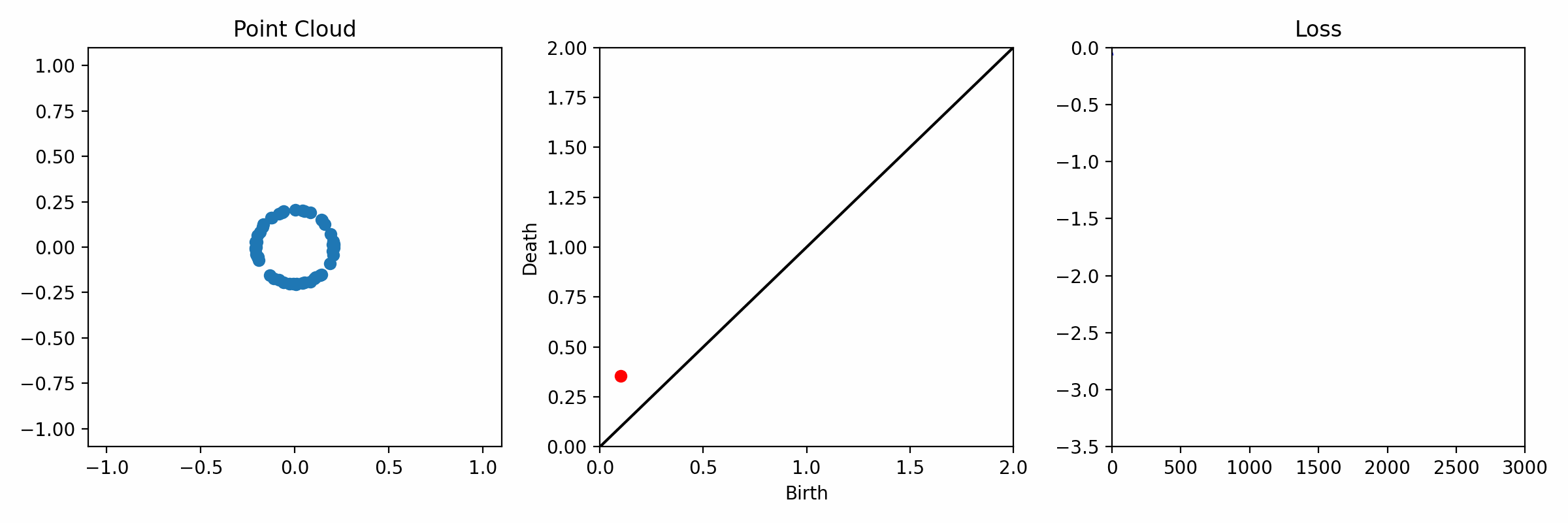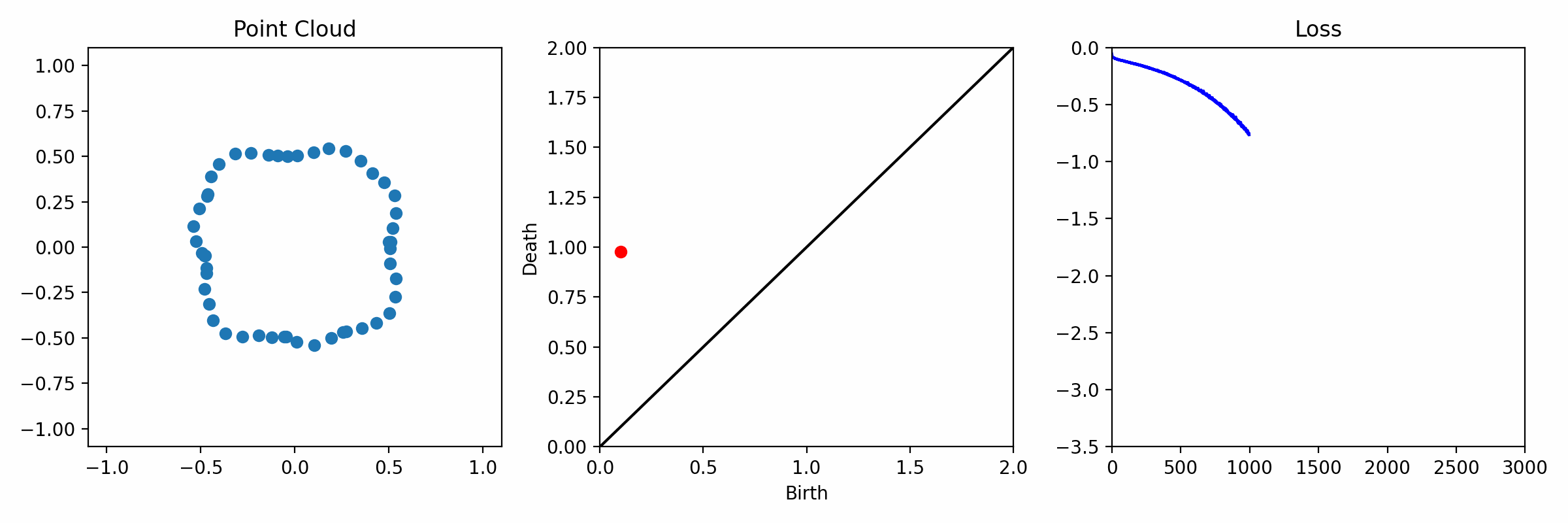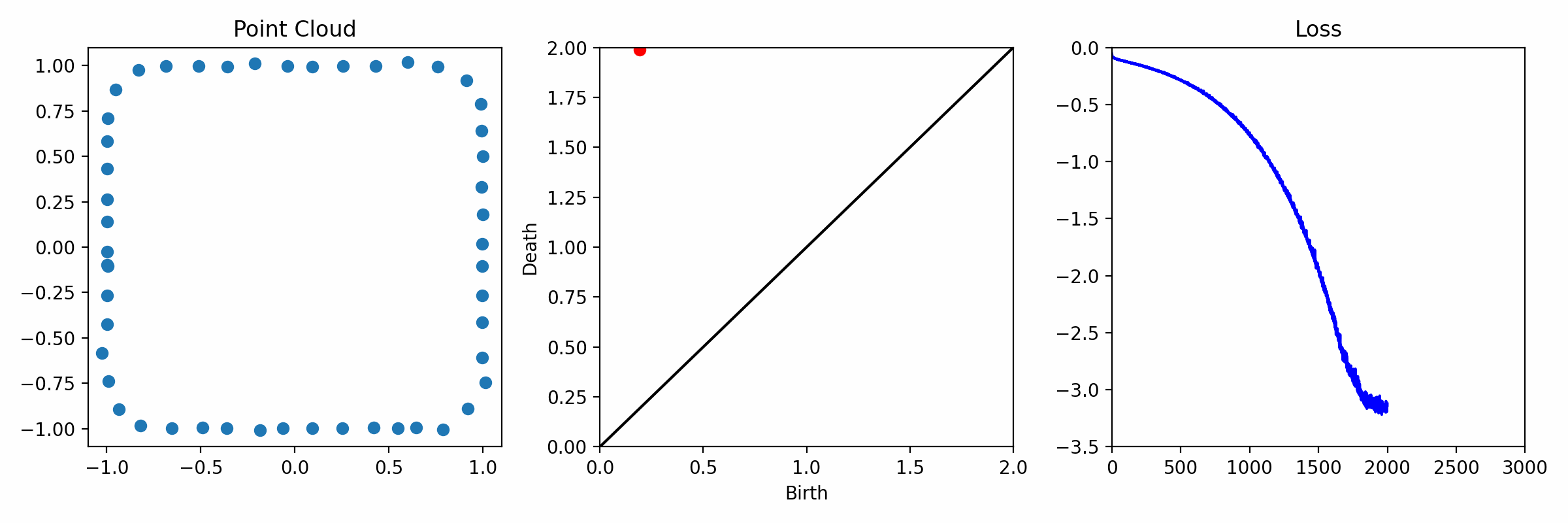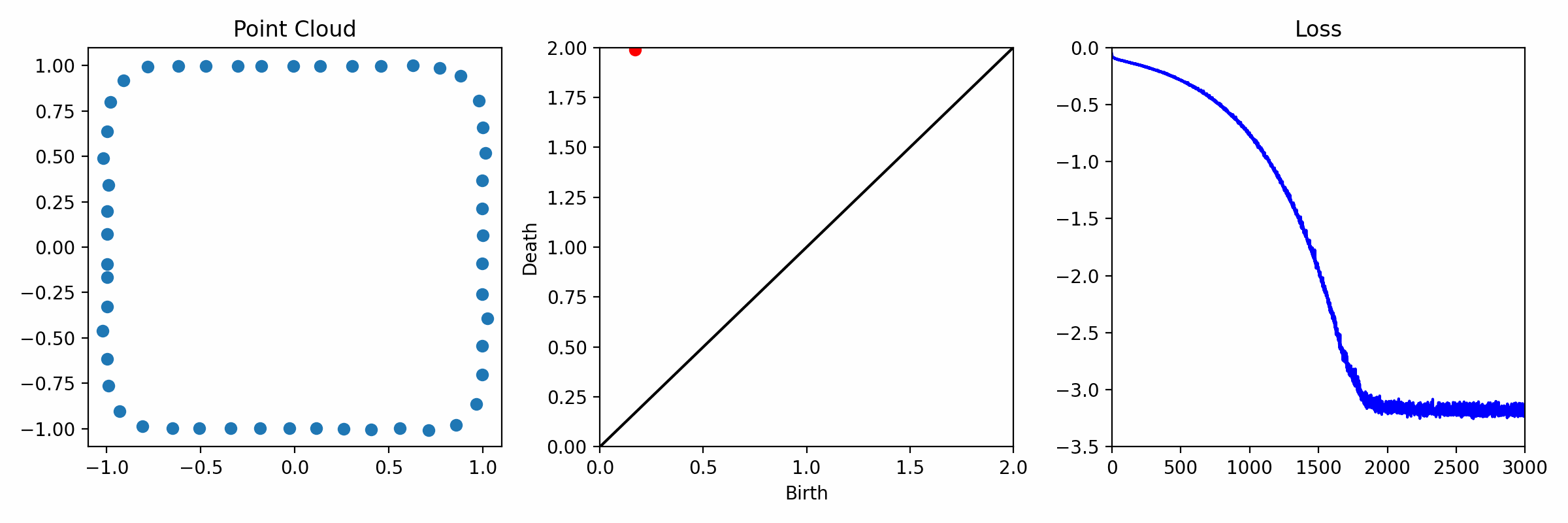 .footnote[Carriere, Mathieu, et al. "Optimizing persistent homology based functions." International conference on machine learning. PMLR, 2021. ] --- # Persistence Optimization Examples .pull-left[ - Expanding loops<br> - Lifetime Restriction<br> - Regularization<br> <br><br><br><br><br><br><br> - Expanding loops<br> - Lifetime Restriction<br> - Regularization<br> - <font color="red">Minimize Entropy</font> ]   ??? Here are two more examples of persistence optimization where I promote larger loops in the point cloud using total persistence along with penalizing persistence lifetimes above the blue line. The bottom example also implements an entropy term to minimize the persistent entropy. We see that the entropy term results in fewer loops in the resulting point cloud. --   --- # Optimal Parameter Space Paths  ??? Now I will present my first proposed application of persistence optimization by applying this idea to dynamical system parameter space navigation. --- # Connection with Dynamical Systems  ??? I plan to utilize this persistence differentiability framework in connection with dynamical systems by leveraging the inherent connection between topology and dynamical systems to guide a system to a more desirable behavior by optimally varying system parameters. The example shown here demonstrates this process by showing the change in persistence diagrams would look like when moving from a chaotic to a periodic response in the parameter space. --- # Persistence Criteria  ??? This will be accomplished by creating a dictionary of persistence based cost function terms to allow for a response to be modified by performing persistence optimization. The first example shown here demonstrates limiting the size of a loop in the persistence diagram which would correspond to limiting the amplitude of oscillation. The cost function term in this case could be defined using the maximum persistence feature. The next example could be used to ensure that the system remains at steady state and only an acceptable level of noise is allowed. The state space trajectory in this case would have very localized points and the cost function can be controlled using the maximum persistence feature. The third case will use persistent entropy to encourage the system to move away from chaotic states to periodic. One example of how this could appear in the state space is shown here where a single large loop is encouraged. The cost function term here would be to minimize the persistent entropy. This leads to my first goal on this project which is to develop a library of these cost function terms that map to specific dynamical system behaviors and allow for intuitive loss function engineering for achieving desired behaviors. --  --  -- 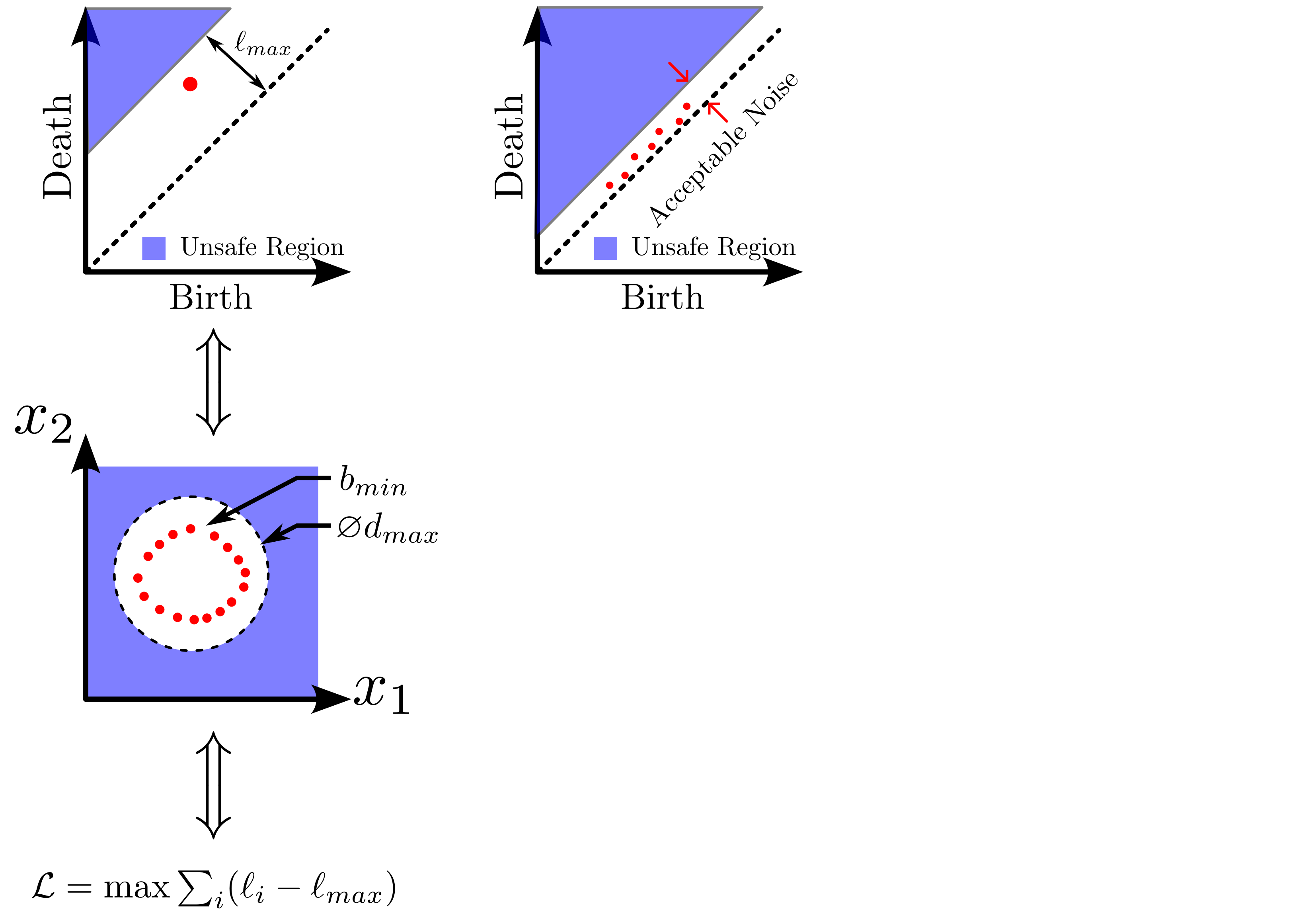 -- 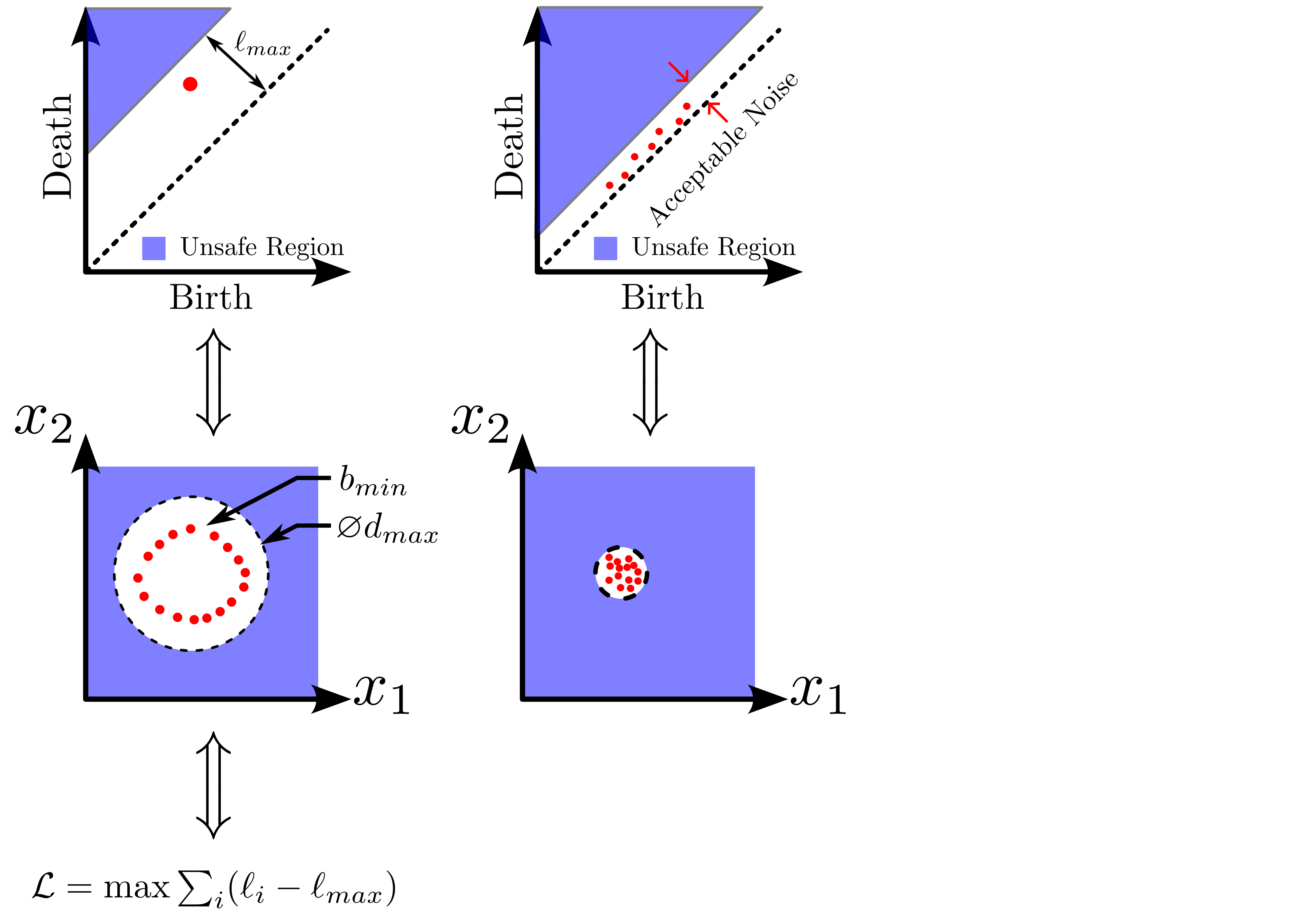 -- 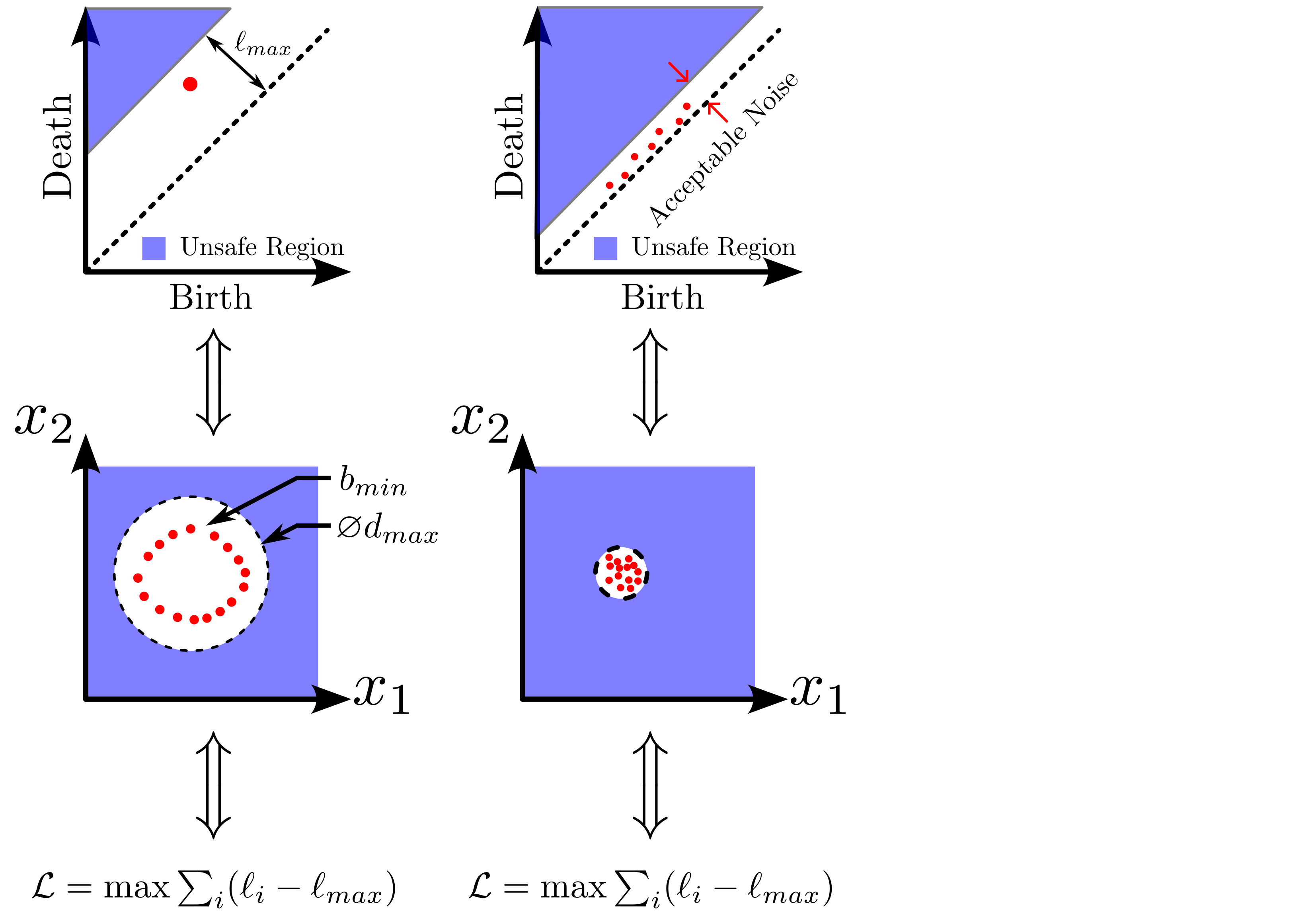 -- 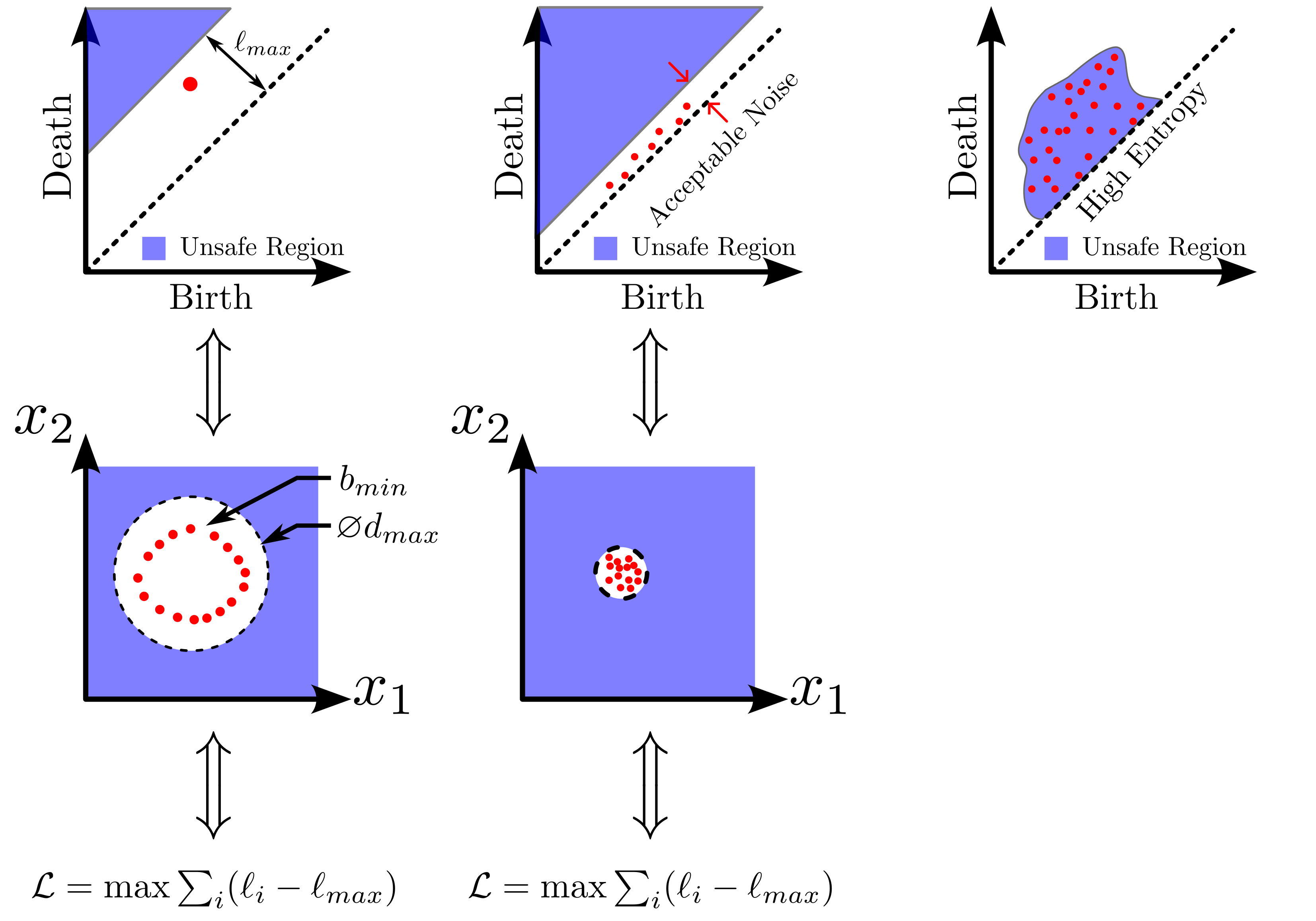 -- 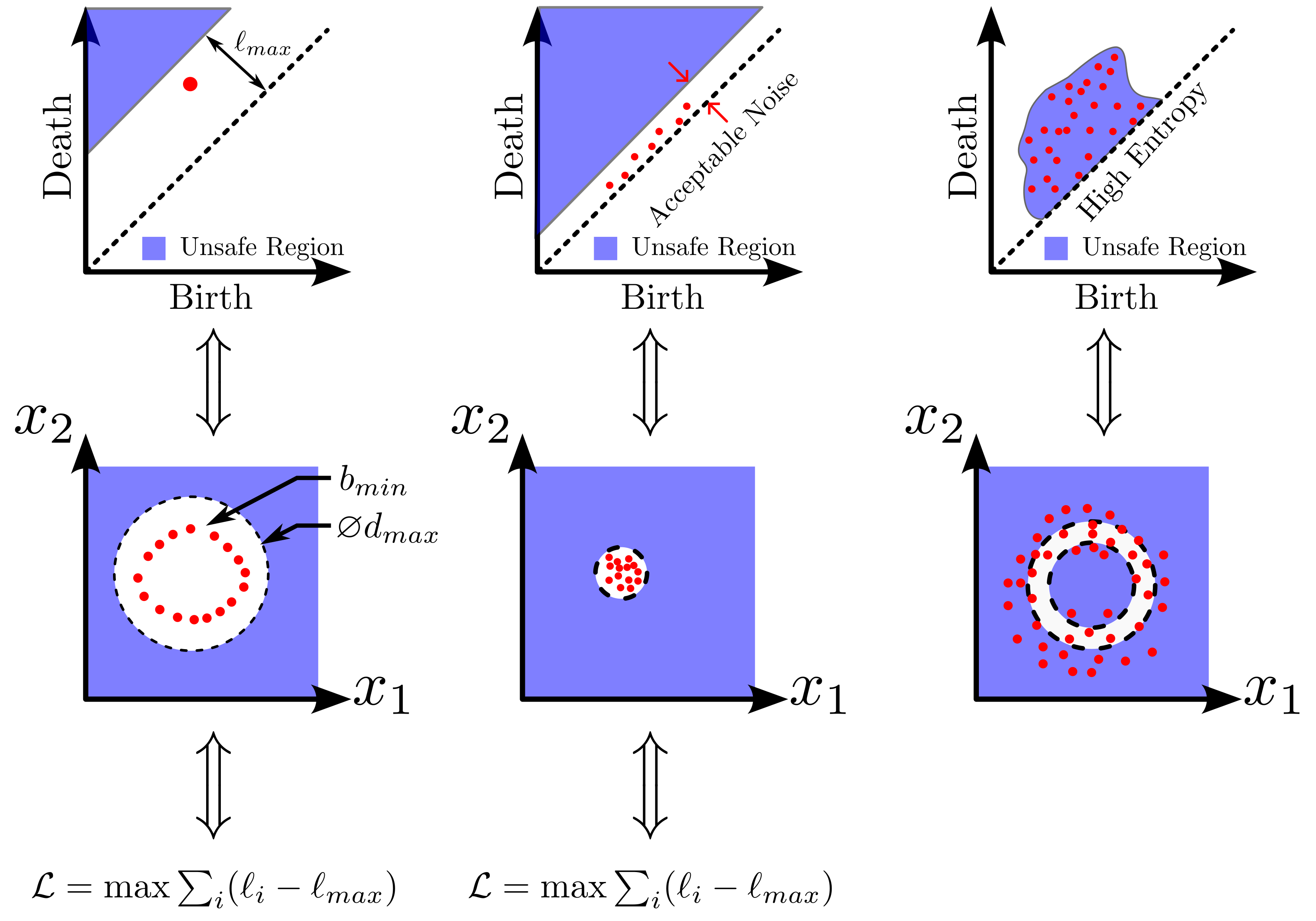 -- 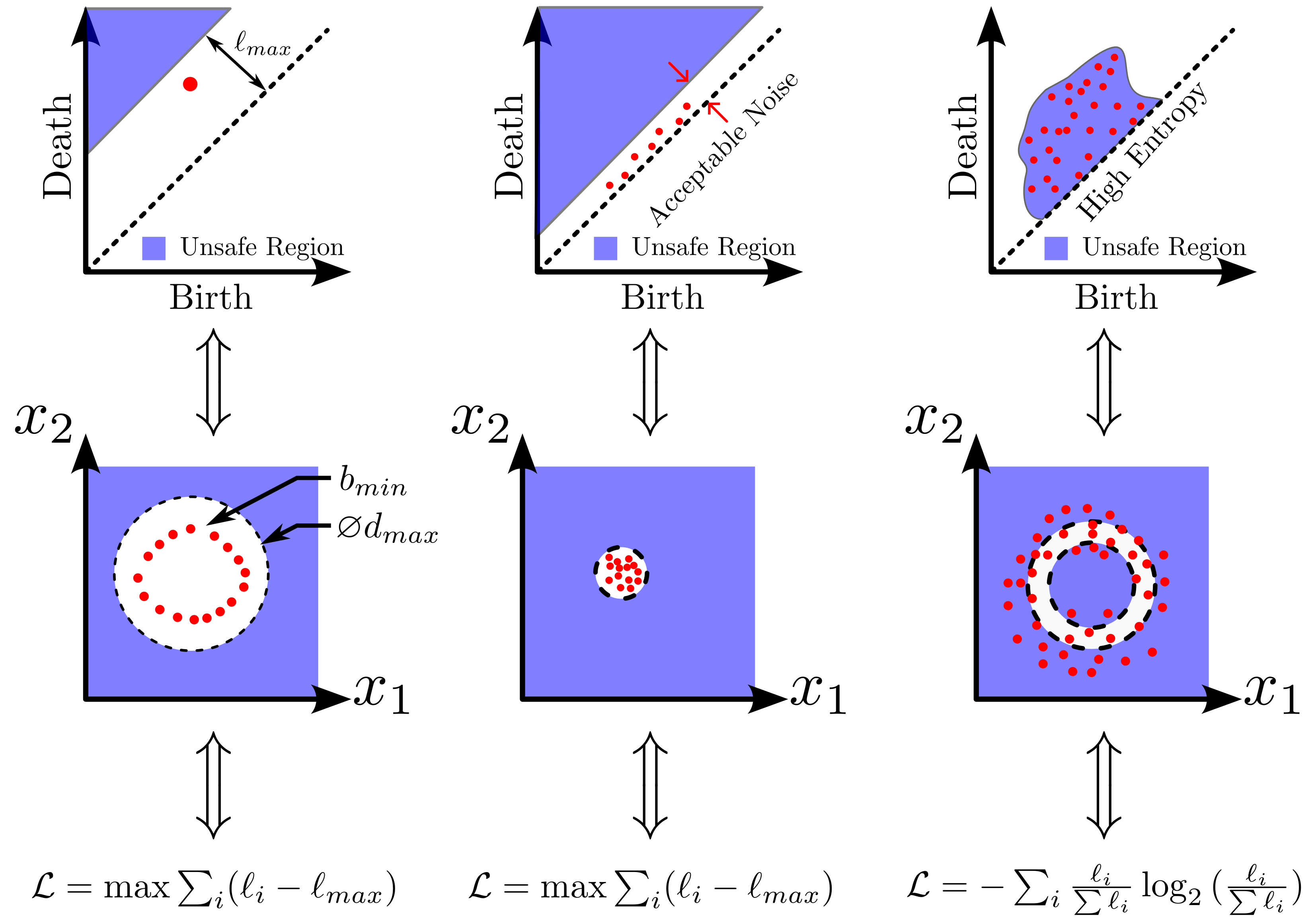  --- # Preliminary Results (Lorenz System) 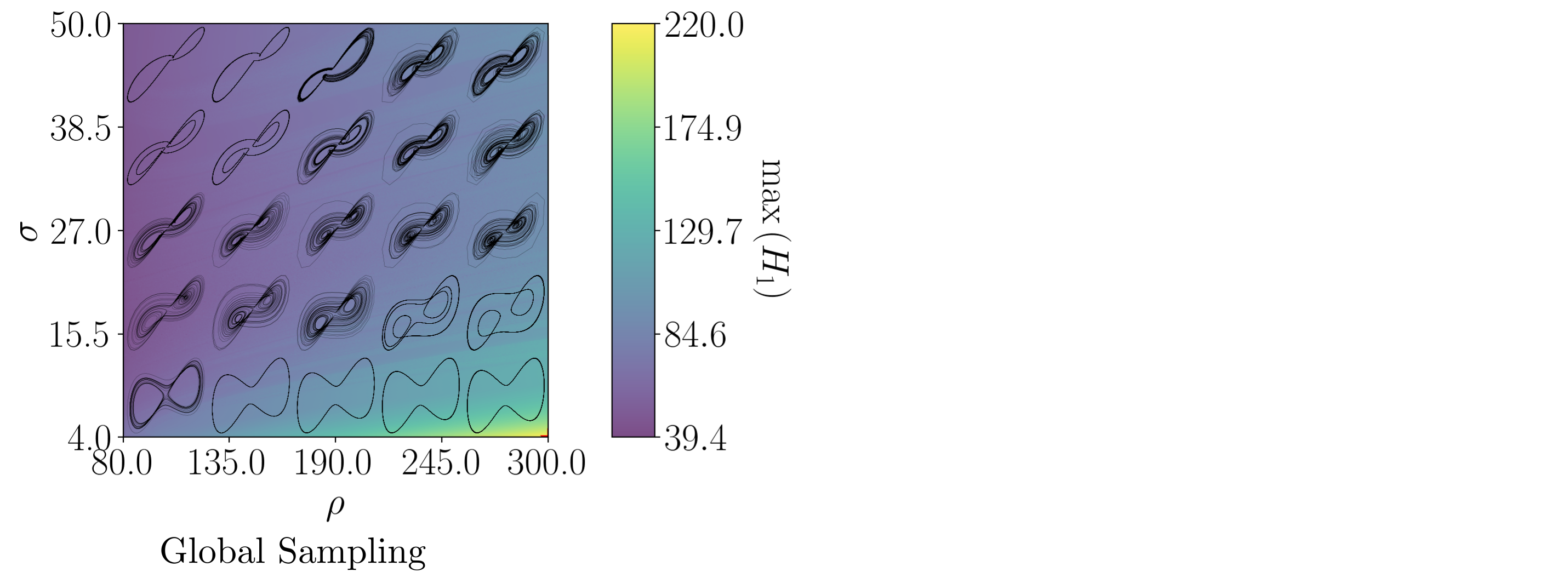 ??? I generated preliminary results by precomputing the maximum persistence feature over a region of the parameter space of the lorenz system. I then chose two derivative free optimization approaches by sampling the maximum persistence feature near a starting point. The goal here was to reach the most periodic solution in the lower right corner. The first sampling method located path points by centering a rectangle around the starting point and moving to the largest maximum persistence feature within that rectangle. The rectangle size was increased and the process was continued until the global maximum was reached. Doing this results in this path. However, it is not ideal to sample over a very large region of the space because in high dimensional spaces this becomes inefficient. For the second sampling method, I chose to sample a small region centered around the current point and update the size of the rectangle based on the direction variability in the 5 previous steps. This was based on the assumption that a high variability in path direction corresponded to chaotic regions of the parameter space. Doing this results in a significantly smaller sampling region (shown in blue) and leads to the most periodic solution in the parameter space while moving away from the chaotic region. We can also look at the persistence diagrams at different points along the path to demonstrate the distinct change in topology as the periodic trajectory is reached. I plan to augment the persistence differentiability map from before to study the differentiability of another map B' that maps the parameter space to time series signals. Numerical algorithms will be developed to numerically approximate the derivative of this map to allow for the full inverse problem to be solved and the optimal path to be obtained in the parameter space. -- 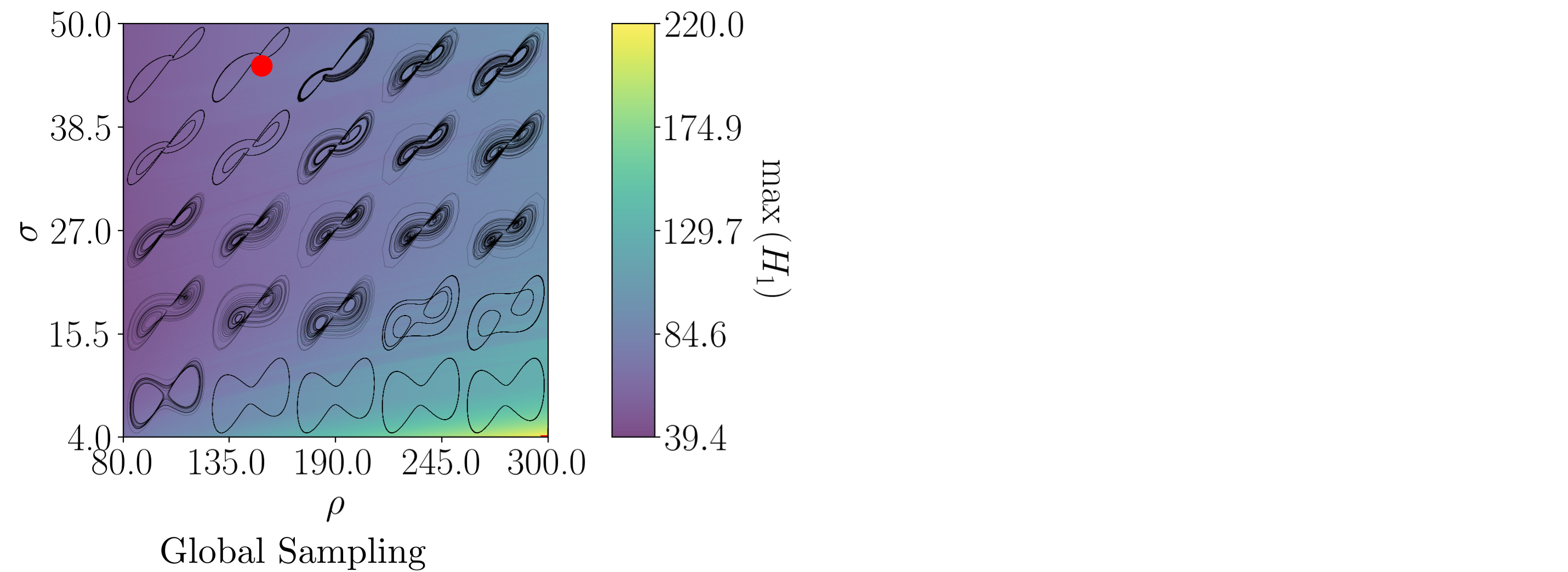 --  --  --  --  --  --  --- # Differentiability of B'  ??? More specifically, if we have a dynamical system parameter space here with 3 parameters a, b and c a point can be chosen in this space which corresponds to a specific point cloud in the state space from simulating the system. For this example the system is two dimensional but in general it can be m dimensional. Computing 1D persistence on this point cloud leads to a single 1D persistence pair at b,d. The persistence diagram is then mapped to a loss function or function of persistence such as maximum persistence. In this case we will say we want to minimize this feature to reduce oscillation amplitude. In order to compute the gradient of the loss function in this case, we need the gradient of the map that takes the parameter space to the point cloud. There are infinitely many directions that can be chosen in the parameter space but the goal is to move in a direction that minimizes the loss function. Approximating B' derivative will allow for taking a step in the loss function space. This will lead to a new persistence diagram, a new point cloud, and consequently a new point in the parameter space. In general the parameter space can be n dimensional. My goal is to develop a numerical method to approximate the derivative of the map B' to optimally move through the parameter space. The animation here shows how the persistence pair moves in the persistence diagram for the rossler system trajectory. As the parameter changes, the size of the attractor changes which agrees with the change in the persistence pair. In this case, using the maximum persistence feature would allow for optimally changing the rossler system parameters to reach a state with limited amplitude oscillations. --  --  --  --  --  --  --  --  --   --- count: false # Differentiability of B'   ??? More specifically, if we have a dynamical system parameter space here with 3 parameters a, b and c a point can be chosen in this space which corresponds to a specific point cloud in the state space from simulating the system. For this example the system is two dimensional but in general it can be m dimensional. Computing 1D persistence on this point cloud leads to a single 1D persistence pair at b,d. The persistence diagram is then mapped to a loss function or function of persistence such as maximum persistence. In this case we will say we want to minimize this feature to reduce oscillation amplitude. In order to compute the gradient of the loss function in this case, we need the gradient of the map that takes the parameter space to the point cloud. There are infinitely many directions that can be chosen in the parameter space but the goal is to move in a direction that minimizes the loss function. Approximating B' derivative will allow for taking a step in the loss function space. This will lead to a new persistence diagram, a new point cloud, and consequently a new point in the parameter space. In general the parameter space can be n dimensional. My goal is to develop a numerical method to approximate the derivative of the map B' to optimally move through the parameter space. The animation here shows how the persistence pair moves in the persistence diagram for the rossler system trajectory. As the parameter changes, the size of the attractor changes which agrees with the change in the persistence pair. In this case, using the maximum persistence feature would allow for optimally changing the rossler system parameters to reach a state with limited amplitude oscillations. --- # Applications  ??? There are many potential applications for optimal parameter space navigation. First, it could be used in medical applications such as studying epileptic seizures, electrical circuits, studying analytical systems such as what I did with the lorenz system on the previous slide and aerospace applications like avoiding aircraft upset dynamics. The main motivating application for this work was on hall effect thrusters so that will be my focus for experimental validation. --  .footnote[1. Nevado-Holgado, et al. Characterising the dynamics of EEG waveforms as the path through parameter space of a neural mass model: Application to epilepsy seizure evolution 2. Erhardt, André Bifurcation Analysis of a Certain Hodgkin-Huxley Model Depending on Multiple Bifurcation Parameters 2018-06 Mathematics 3. Gill, Stephen J. et al. Coetzee, Etienne Upset Dynamics of an Airliner Model: A Nonlinear Bifurcation Analysis 4. Hassona, Salama et al. Time series classification and creation of 2D bifurcation diagrams in nonlinear dynamical systems using supervised machine learning methods. ] --  --  --  --  --- # Hall Effect Thrusters  ??? I will now give an overview of hall effect thrusters or HETs and motivate the need for parameter space navigation. Hall effect thrusters are a class of ion thrusters that generate thrust for a space craft by accelerating ions through an electromagnetic field. The diagram on the left shows a side view of the thruster with some solar panels for reference. The thruster contains an anode and cathode labeled here by a and c. The anode and cathode are connected in a circuit with a discharge voltage Vd that results in a discharge current Id. An axial electric field is induced using an outer coil of wire and a corresponding radial magentic field is also induced. Ionized gas (typically xenon) is injected into the thruster which is accelerated through the electric field to generate thrust. These thrusters can exhibit some undesirable dynamics such as high amplitude low frequency breathing mode oscillations in the thrust leading to suboptimal performance. Another undesirable behavior occurs when some of the high energy ionized particles cause erosion of critical surfaces on the thruster and the space craft. These operating modes are induced by changes in some of the system parameters so when maneuvering the space craft by changing the parameters it is important to do so optimally and avoid the oscillations. I plan to experimentally validate my parameter space navigation tools on HET data from the air force research lab in california. I will be working with AFRL researchers this summer in my internship specifically simulating and learning more about HETs. --  --  --  --  -- 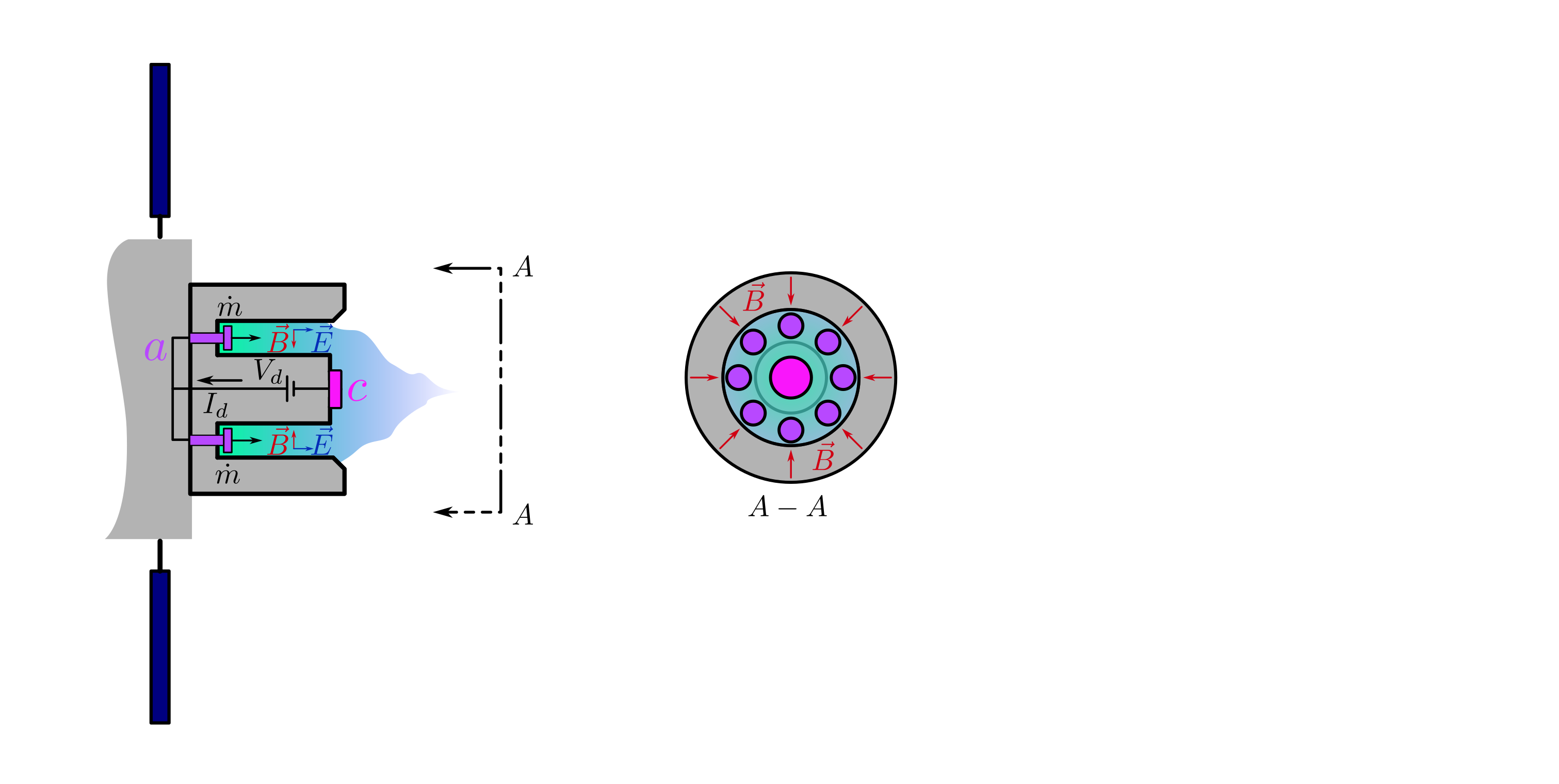 -- 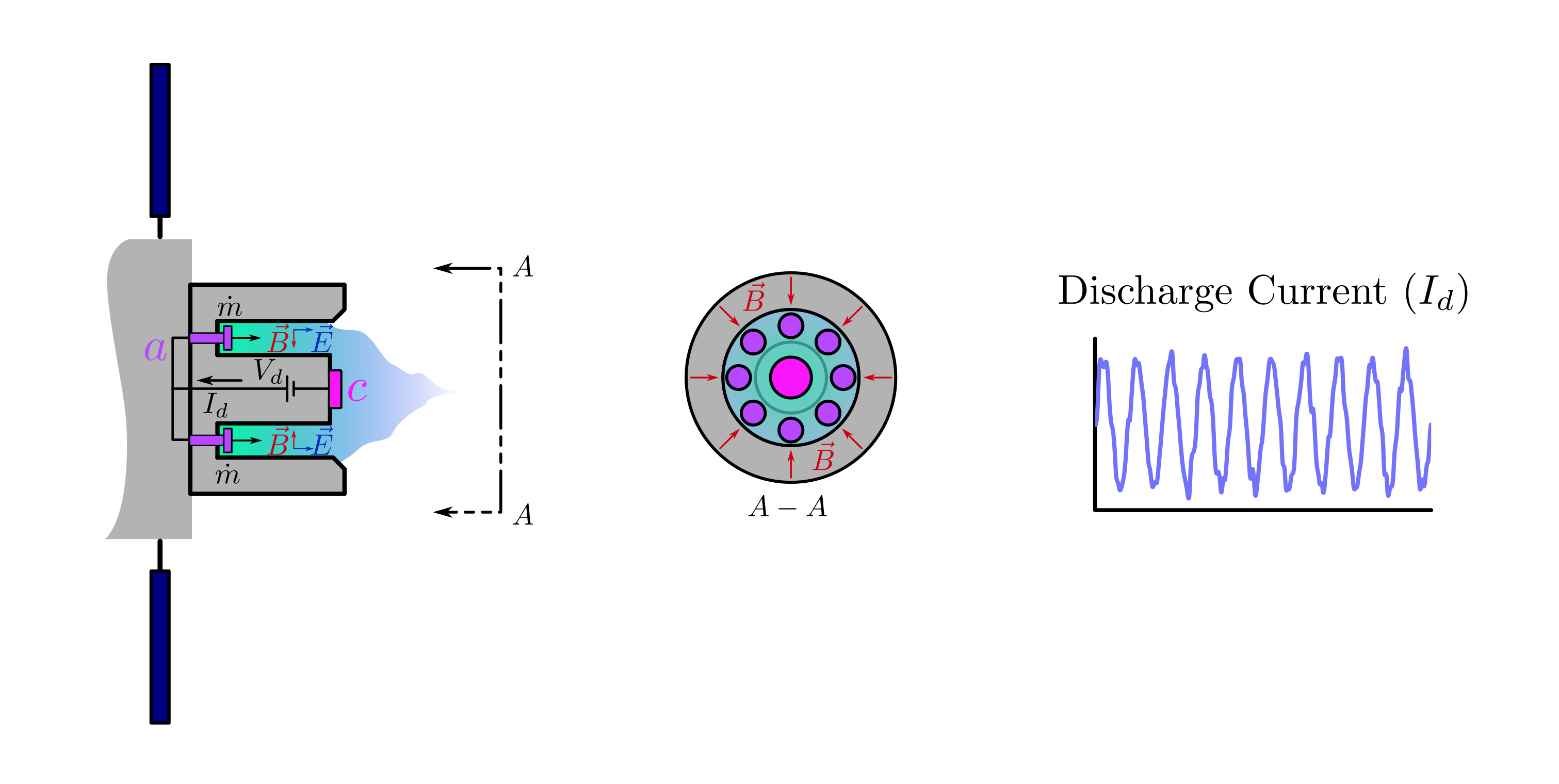 -- 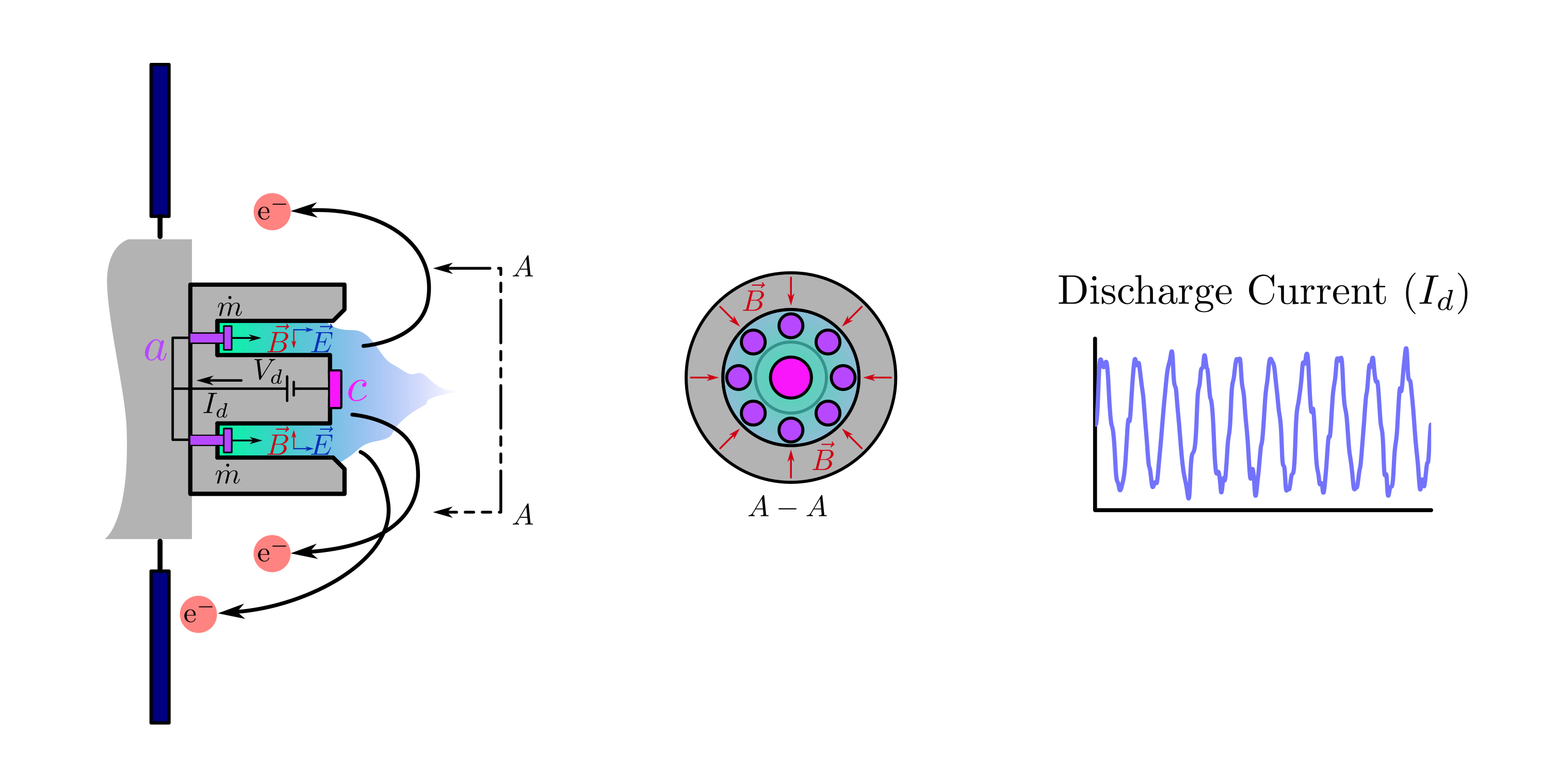 --  --- # Data Assimilation 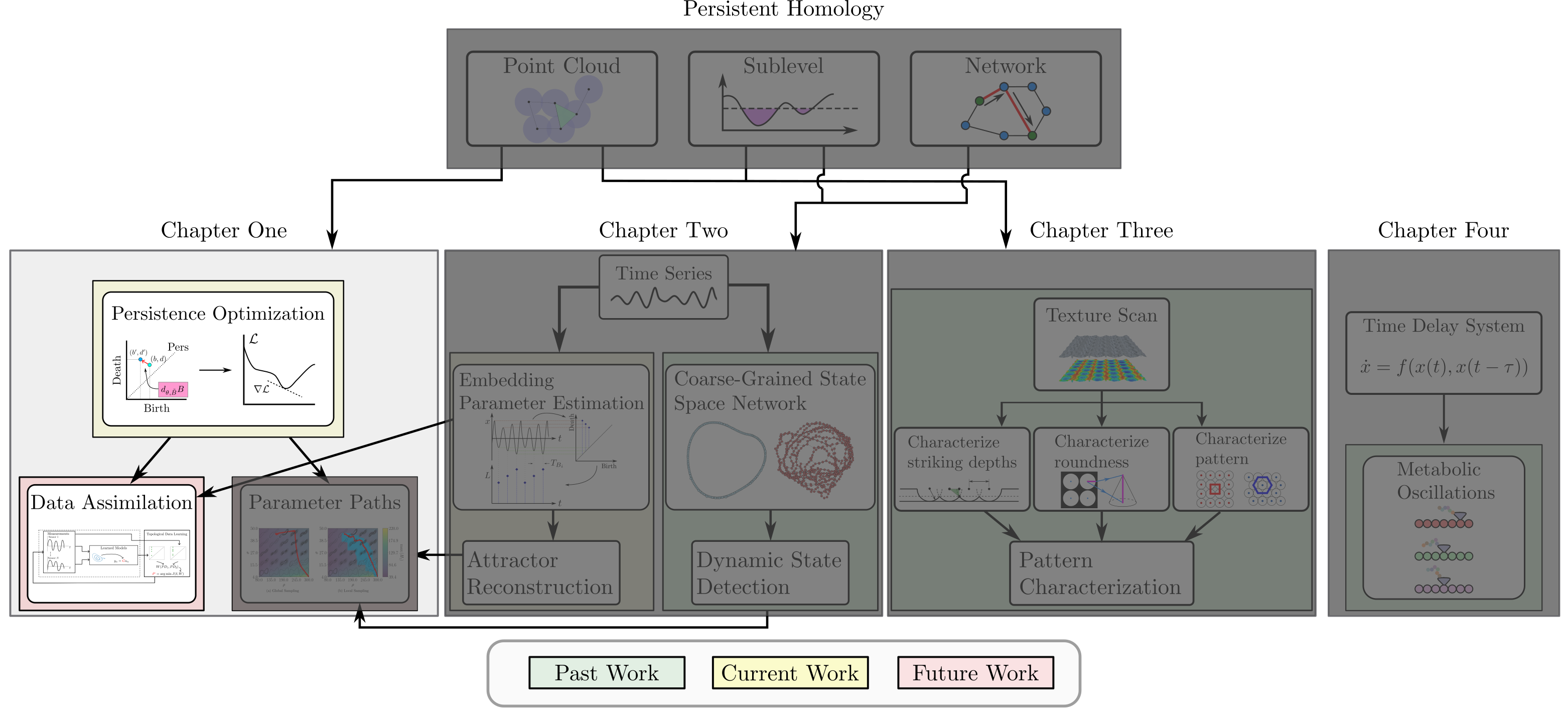 ??? I will now move into my proposed data assimilation framework through the lens of persistence optimization. --- # Classical Time Series Forecasting  ??? Before we can discuss data assimilation, it is important to understand time series forecasting. There are many methods for doing this and here are some of the classical approaches. The autoregressive model works by learning the coefficients phi for the training data with some additive noise to forecast future states of the system. The moving average model learns the coefficients theta based on the average of the signal values before that point. Again this method learns with additive noise. These two methods can be combined using the autoregressive moving average or ARMA model which learns both phi and theta coefficients simultaneously. --  -- 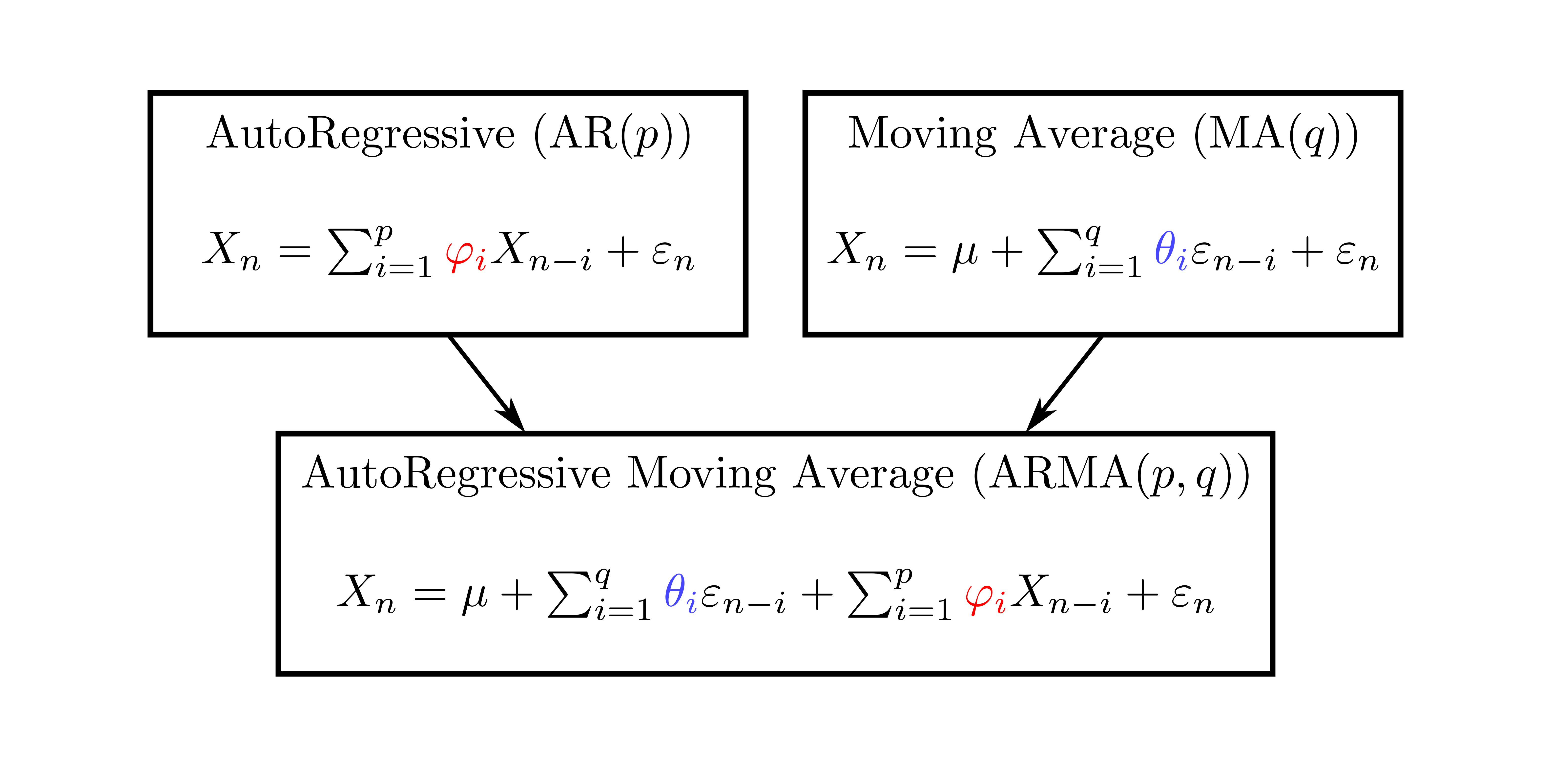 --- # Random Feature Map Forecasting  .footnote[Rahimi, A., & Recht, B. (2007). Random features for large-scale kernel machines. Advances in neural information processing systems, 20.] ??? Another forecasting method is called random feature map forecasting. This method works by assuming we have a D dimensional unknown system. It is assumed that we are only able to obtain noisy observations of the true underlying system. U^o_n is the observation at the nth step and U_n is the true state. Gamma is the measurement covariance matrix and eta is the noise vector. The idea with random feature map forecasting is that we start in a D dimensional space from the measurements and use random feature maps to move to a higher dimensional space with reservoir dimension Dr. The tanh function was used in this work but in general any activation type function that is a function of the weights and bias in this form will work. The weight matrix and bias vector are drawn from uniform distributions and fixed for the training process. These feature vectors exist in a Dr dimensional space and the goal is to learn surrogate model coefficients W_LR in this space using linear ridge regression. These model coefficients form a map from the random feature space to the state space of the system and this map is then used to predict future system states. The cost function here is defined to minimize the differences between the model and observations with regularization. --  -- 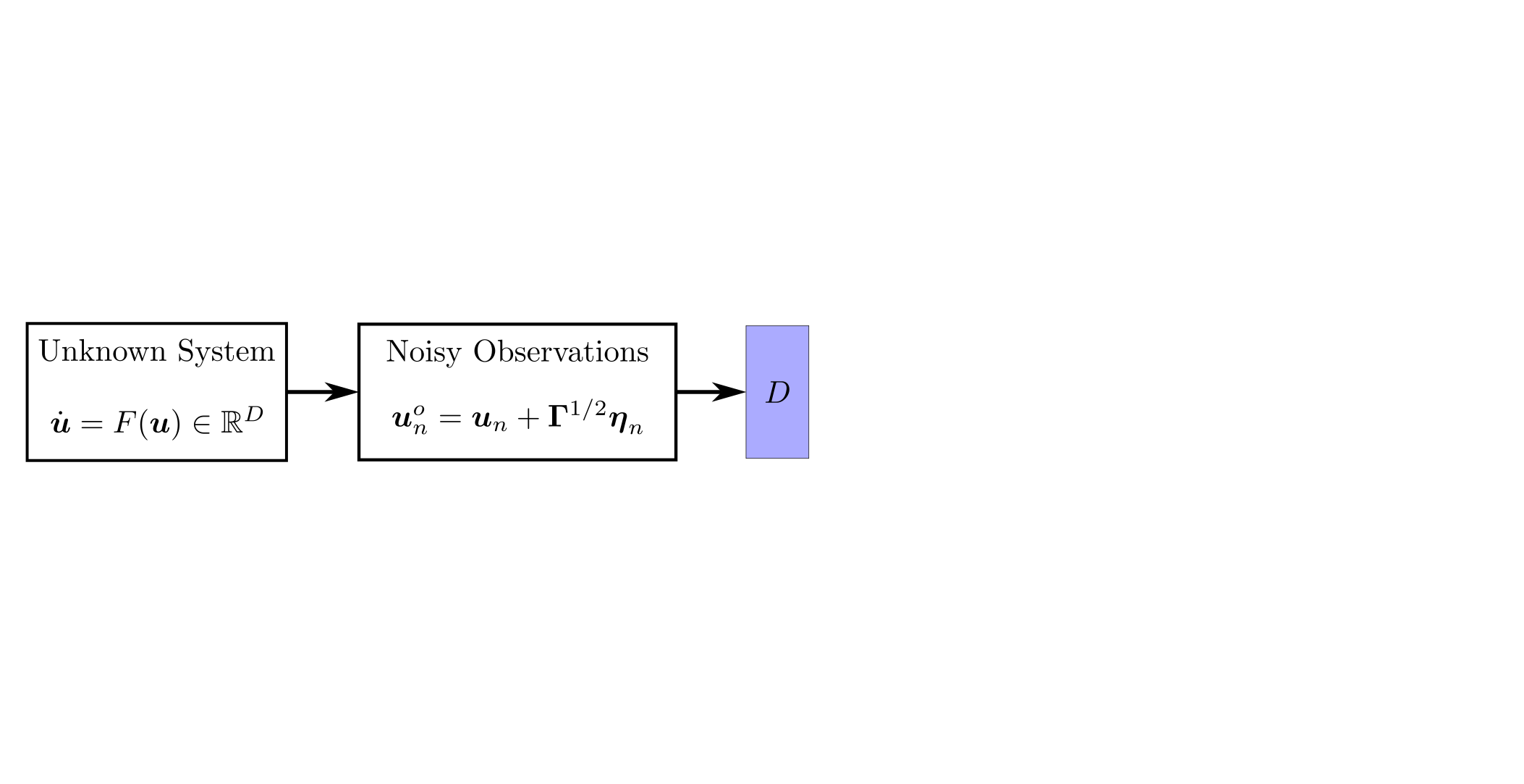 -- 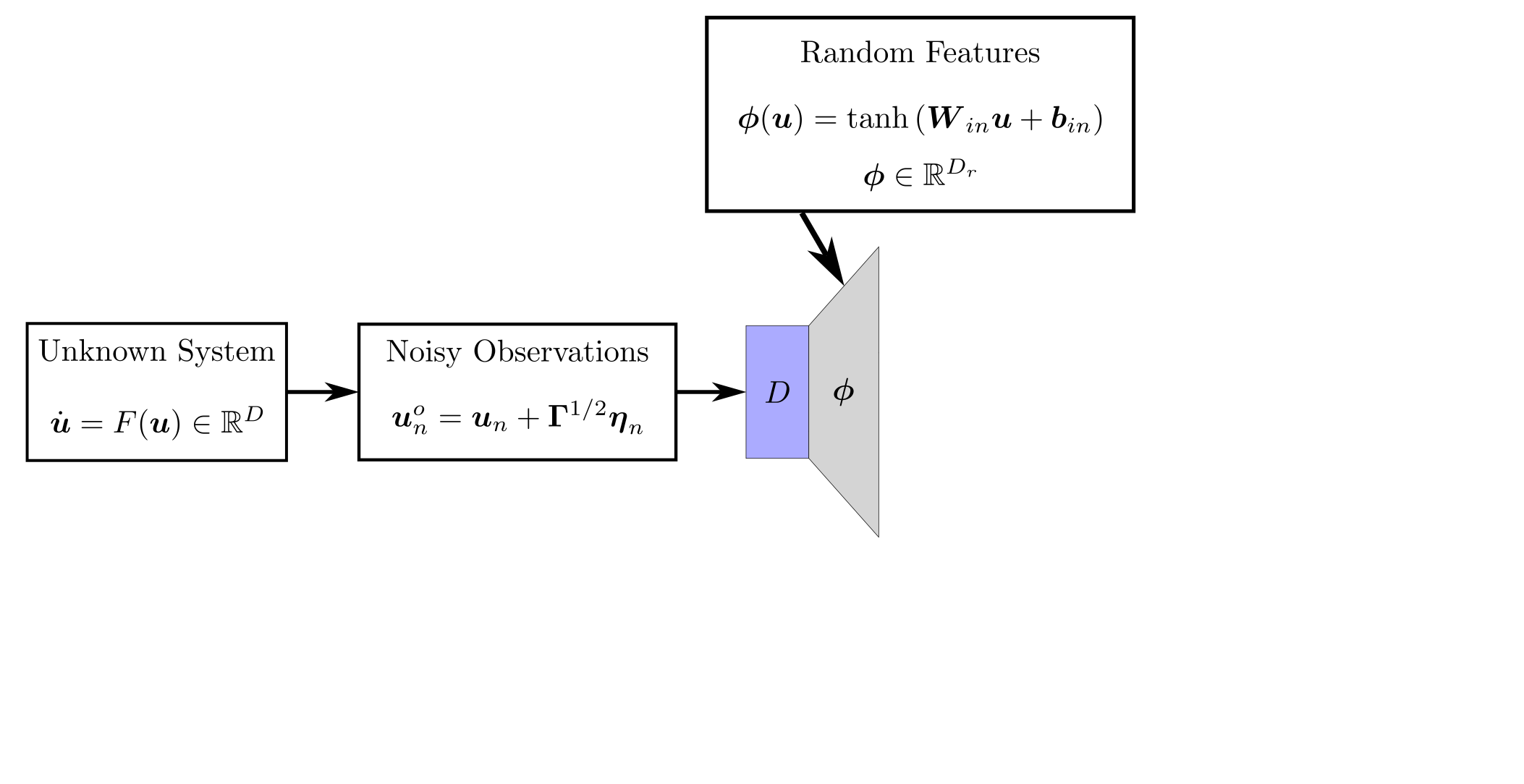 -- 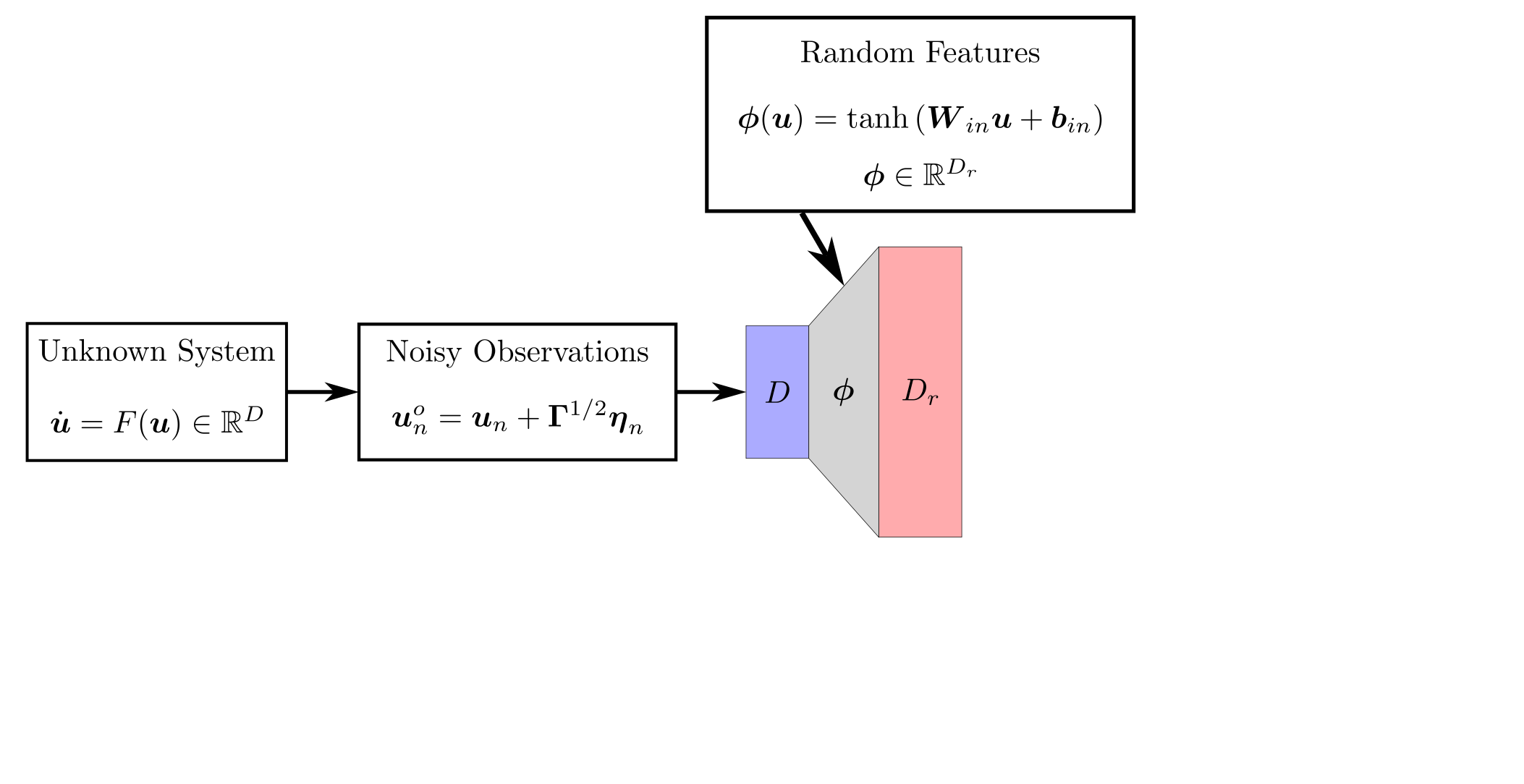 -- 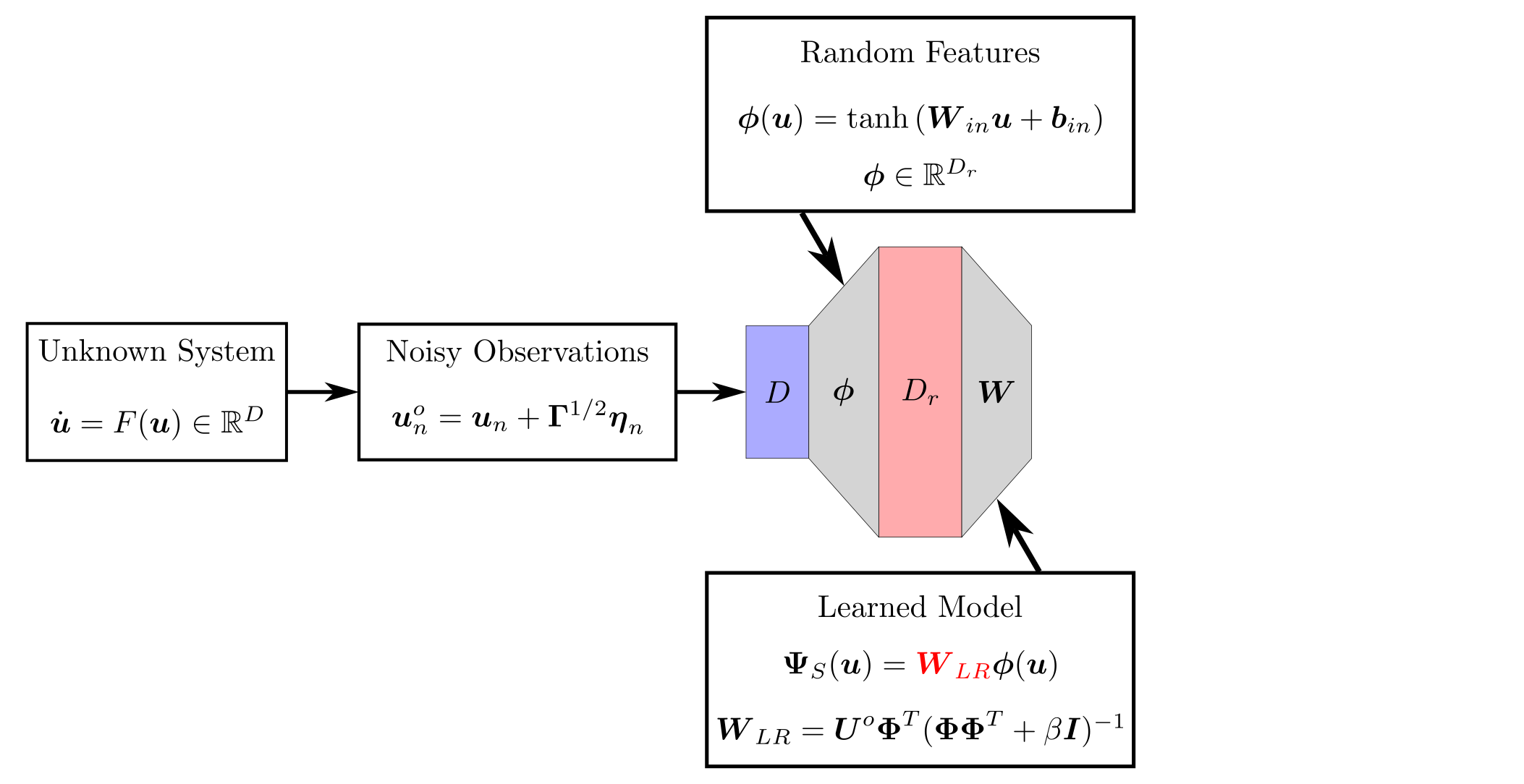 -- 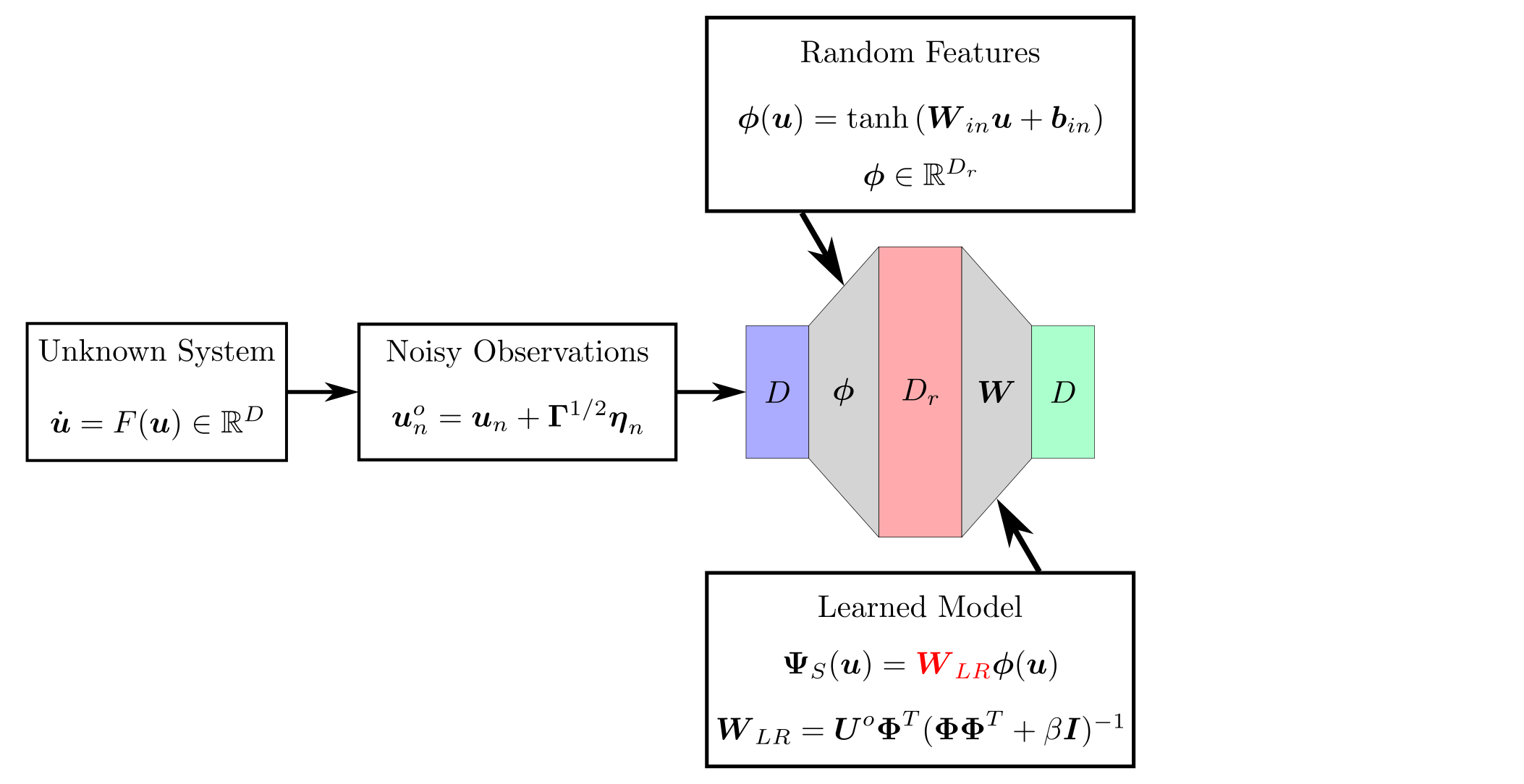 -- 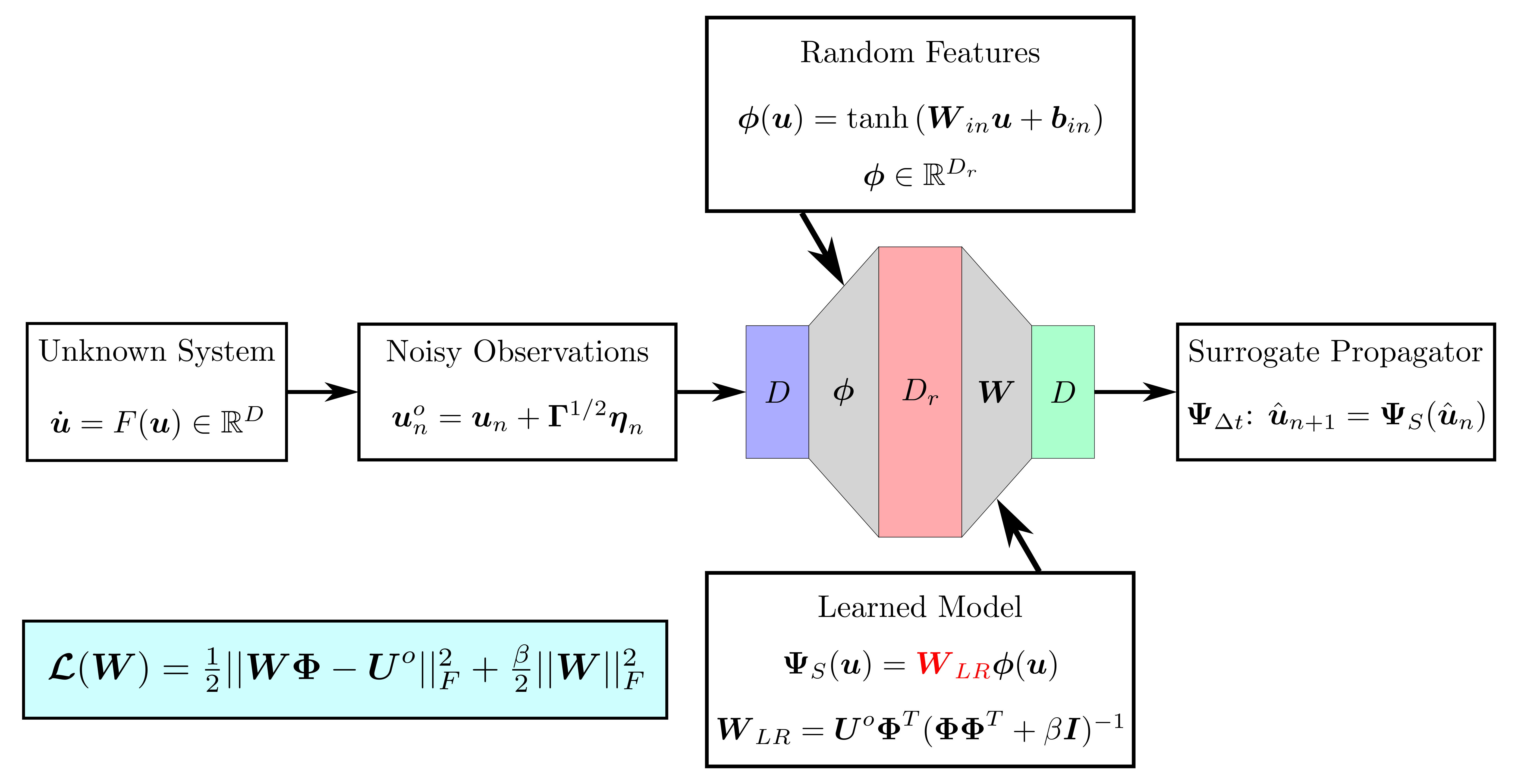 --- # Random Feature Map Example  ??? Here is an example of using random feature map forecasting on the chaotic lorenz system. I chose chaotic parameters for this example and used a reservoir dimension of 500 and sampled the random features from the uniform distributions shown. In general the forecast horizon will be dependent on these distributions and multiple widths should be tested. If I start the simulation, the forecast will begin when the green vertical line appears. The trajectory follows the true trajectory after the forecast begins but as expected begins to deviate over time. This is in the case where there is zero measurement noise. If there is measurement noise present the forecast ability decreases significantly. -- 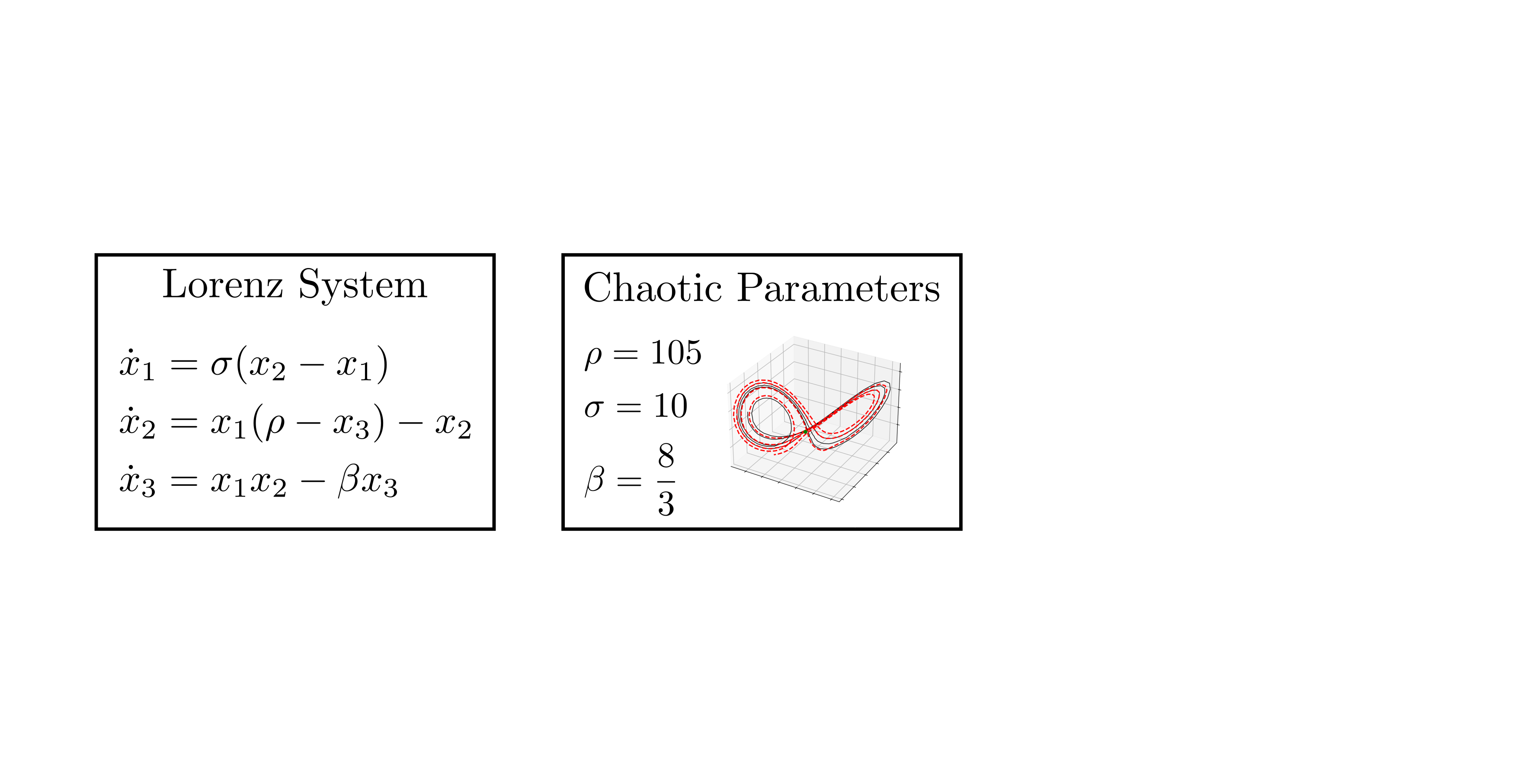 --  --  --- # Data Assimilation Overview  ??? To optimize the forecast horizon in the presence of measurement noise, a concept called data assimilation is used. With data assimilation it is assumed that there is a model for the system that could be obtained from forecasting, and here is a plot of what the model result may look like. If measurements are taken from the system, there are associated uncertainties and these measurements contain useful information for updating the forecast model. The true system state could be the green curve here. In data assimilation, the forecast results are updated based on the difference between the forecast and the measurement result scaled by a gain matrix K. This gain matrix comes from minimizing a cost function to minimize the model and measurement discrepancies based on the respective covariance matrices. This estimation x_a is typically referred to as the analysis. Initially, the model is taken to be the optimal estimation and once a measurement is taken, the model result is updated to be closer to the true system state. As more measurements are taken, the estimation improves and you could imagine that for a high enough sampling rate this would essentially be a continuous curve. -- 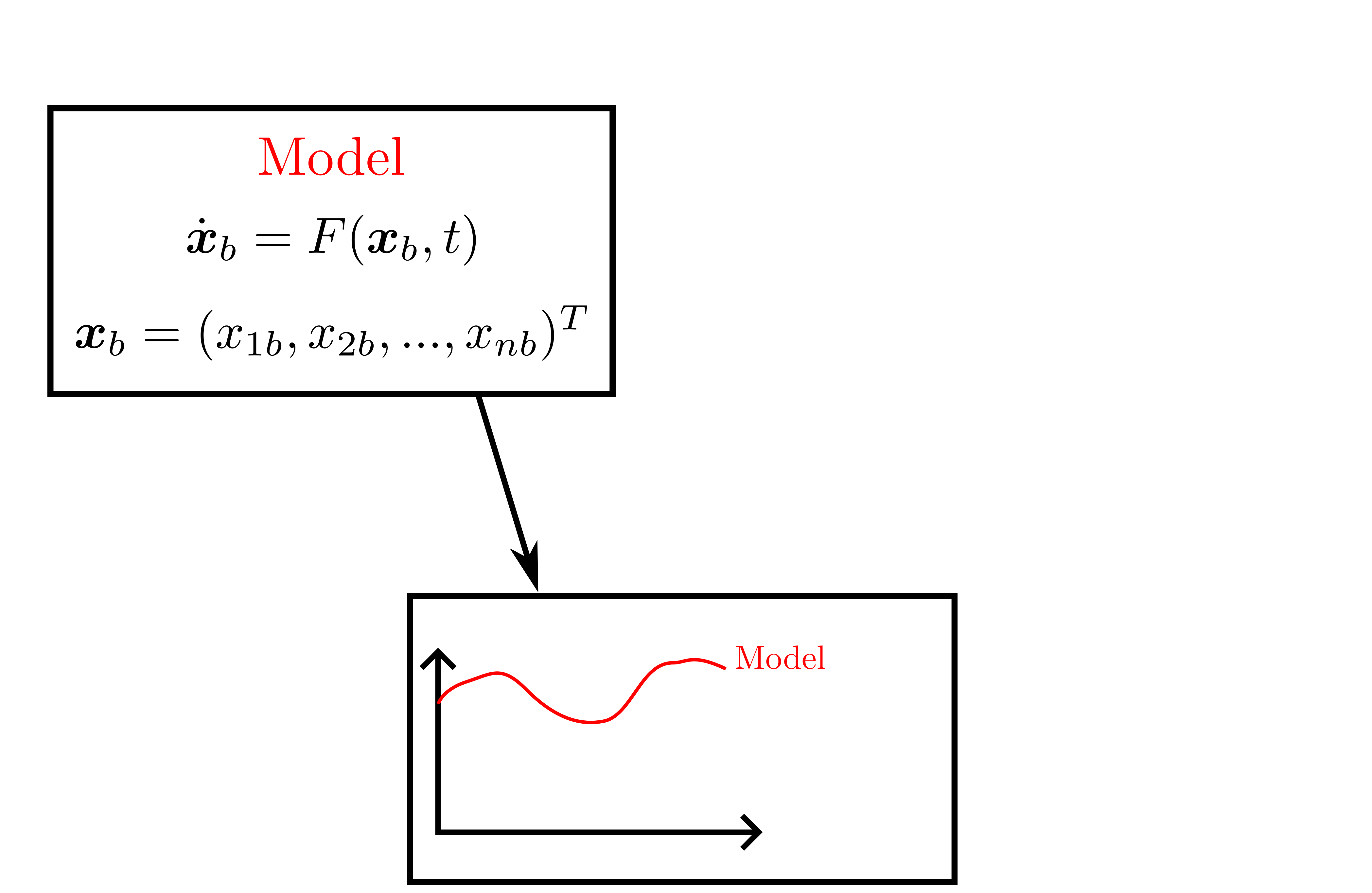 -- 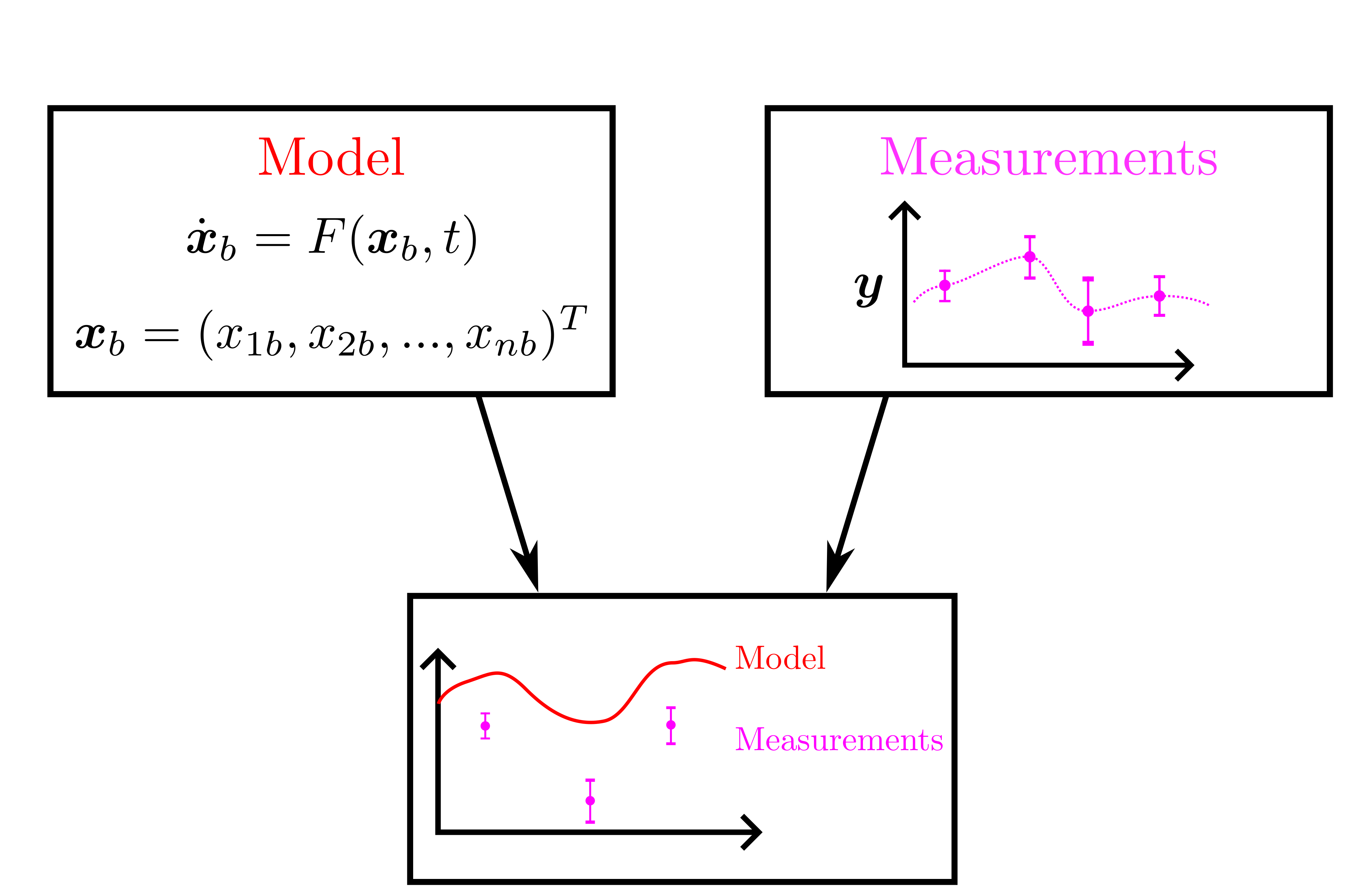 -- 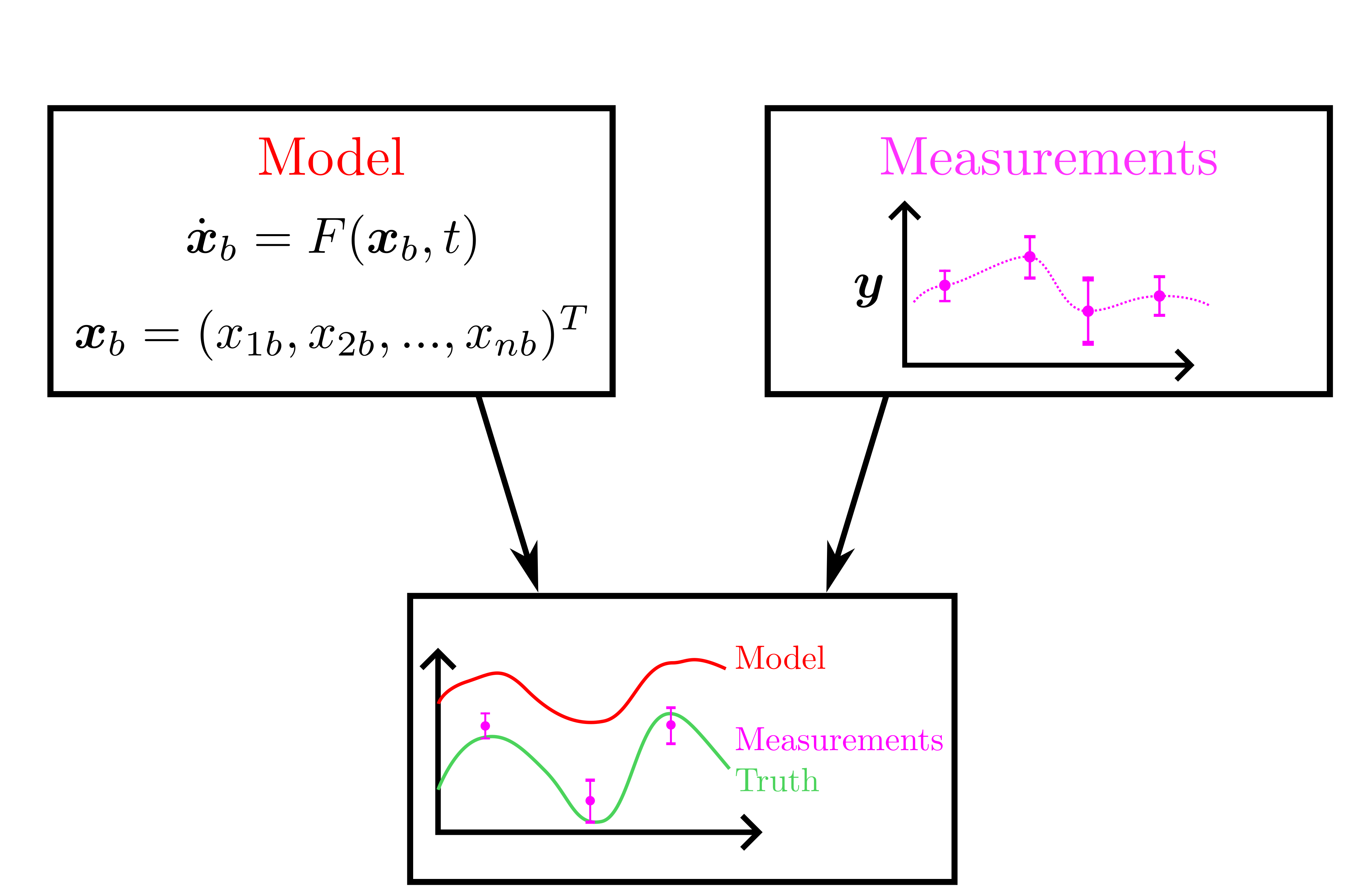 -- 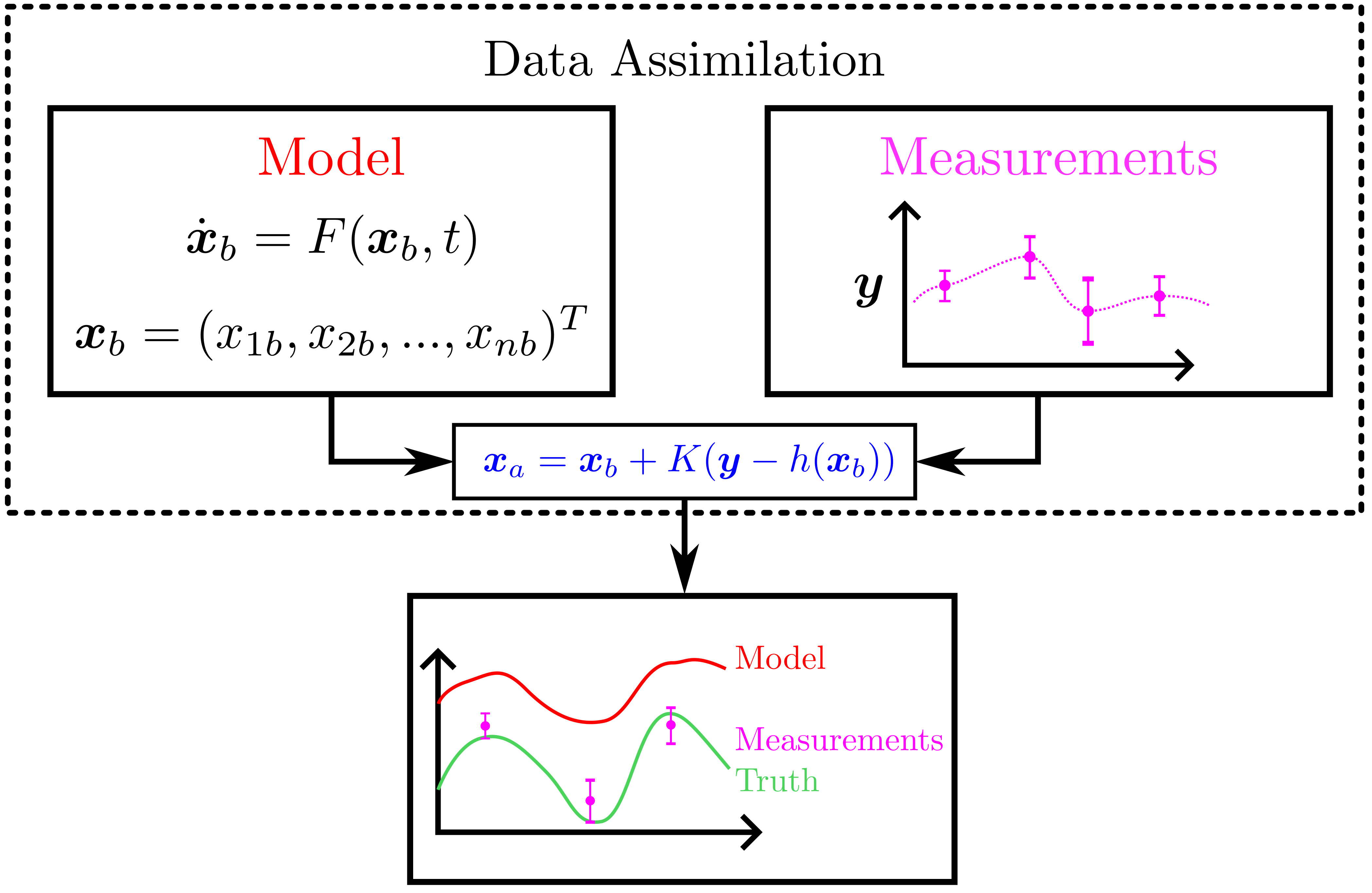 -- 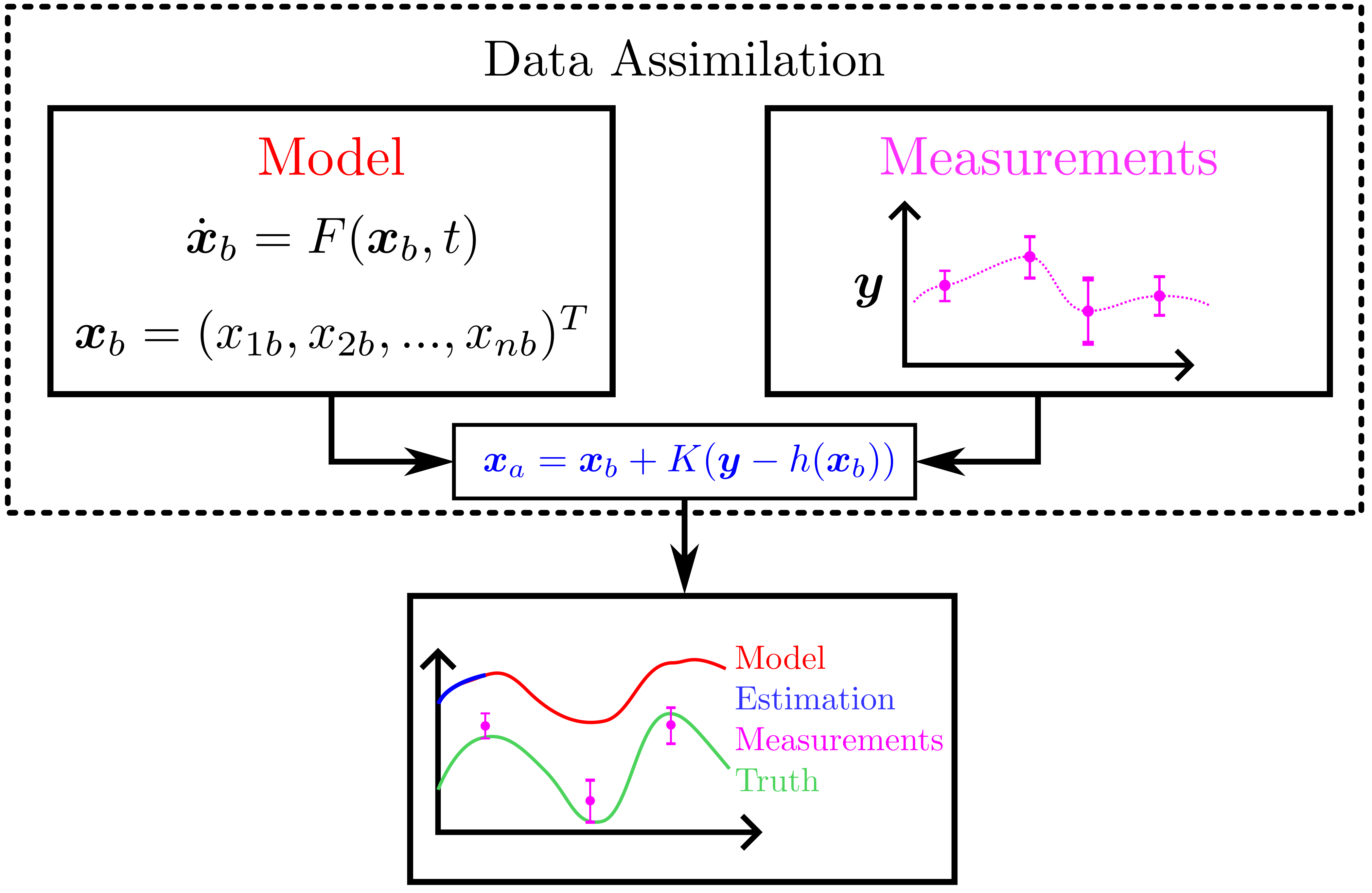 -- 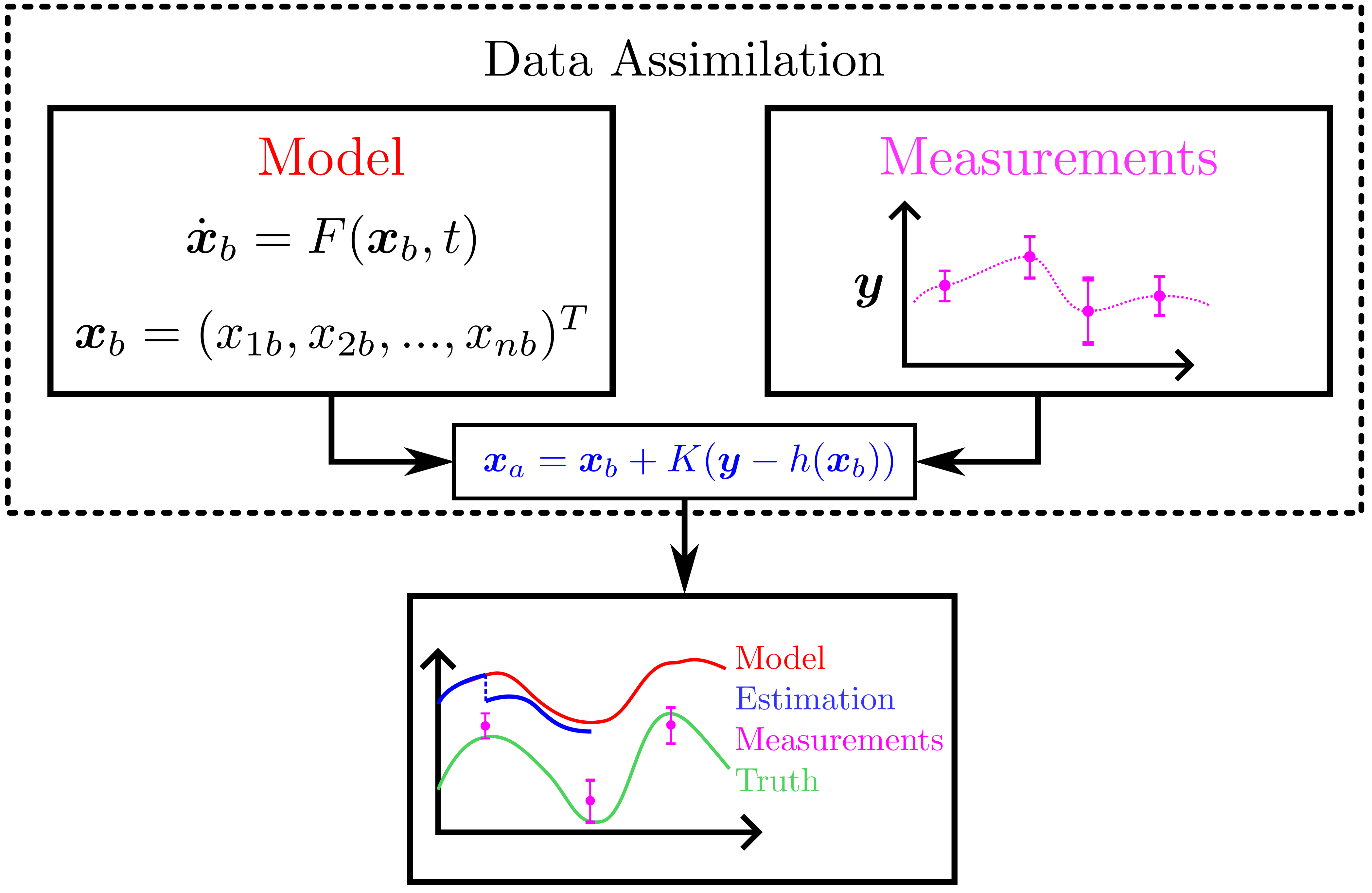 -- 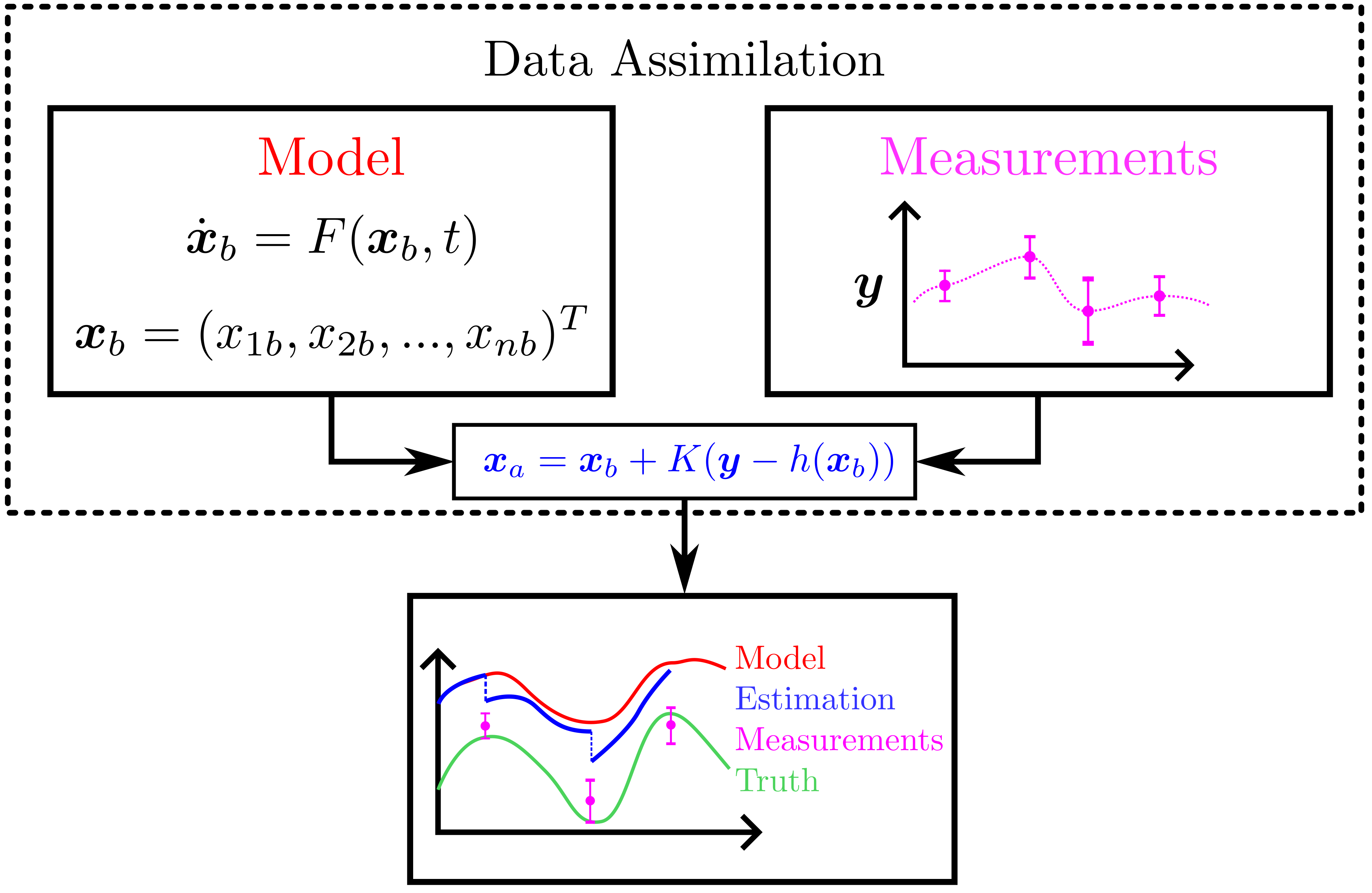 -- 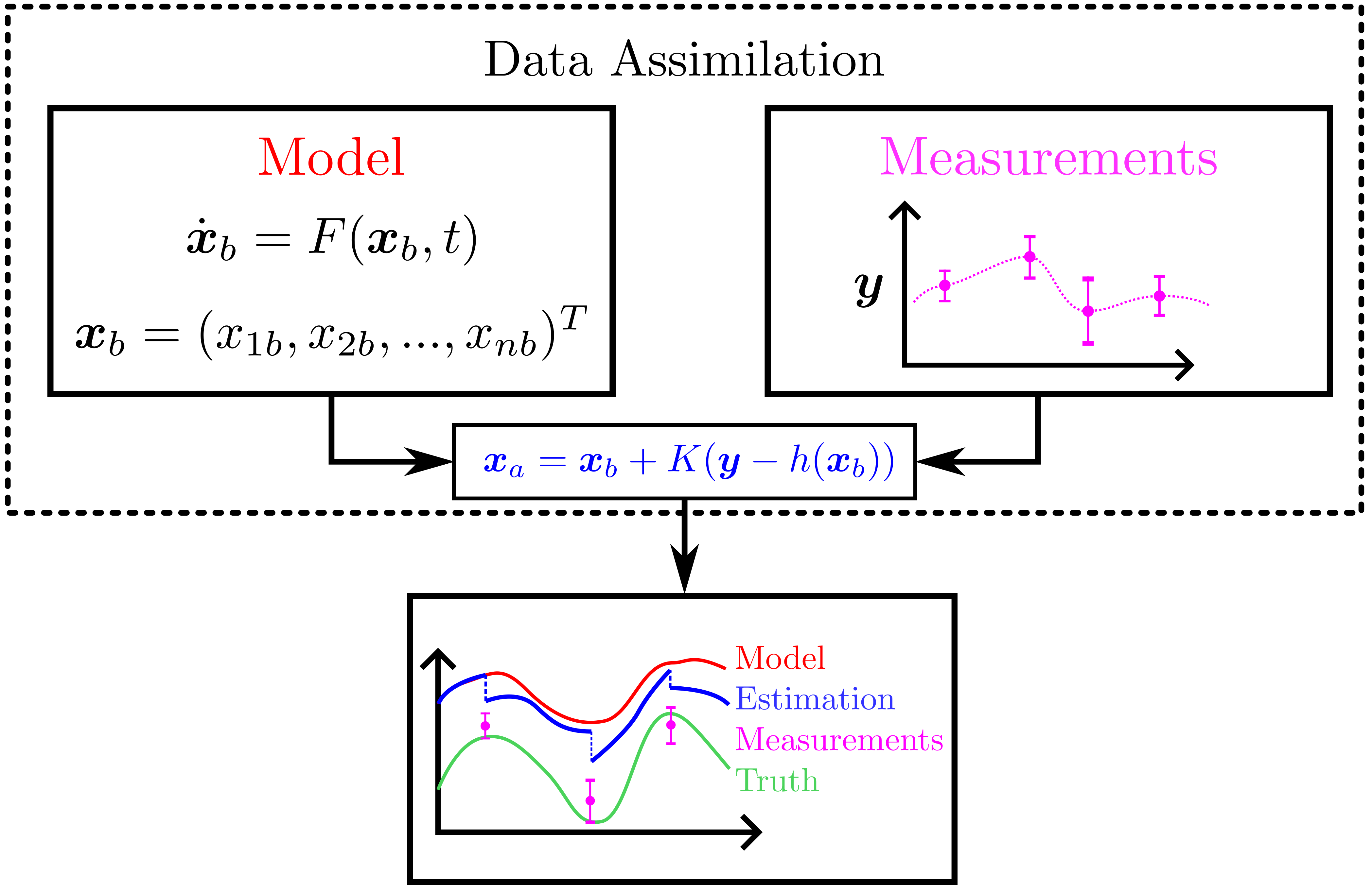 --- # Random Feature Maps and Data Assimilation (RAFDA)  .footnote[Gottwald, G. A., & Reich, S. (2021). Supervised learning from noisy observations: Combining machine-learning techniques with data assimilation. Physica D: Nonlinear Phenomena, 423, 132911.] ??? Data assimilation has been applied to the random feature map forecasting model using an ensemble kalman filter. This method is called random feature maps and data assimilation or RAFDA. The algorithm starts with noisy observations of the system and performs random feature map forecasting to obtain a forecast model. The estimation is then updated by comparing model result and incoming measurements with the kalman filter and this is repeated for M observed samples using the noise statistics to obtain an ensemble of estimations and the average weights can be used for forecasting future states. I will point out that each step requires M samples for each data point and data assimilation is only applied during training. M was taken to be 1000 in the paper at the bottom and I found that it significantly increases computation time compared to the linear regression method. The cost function used for linear regression random feature map forecasting is shown here where the difference between the model and observed states is minimized with regularization. RAFDA does not give an optimizer of this cost function but in the paper introducing this method by Gottwald and Reich, they show that it can give better weights for future unseen data. -- 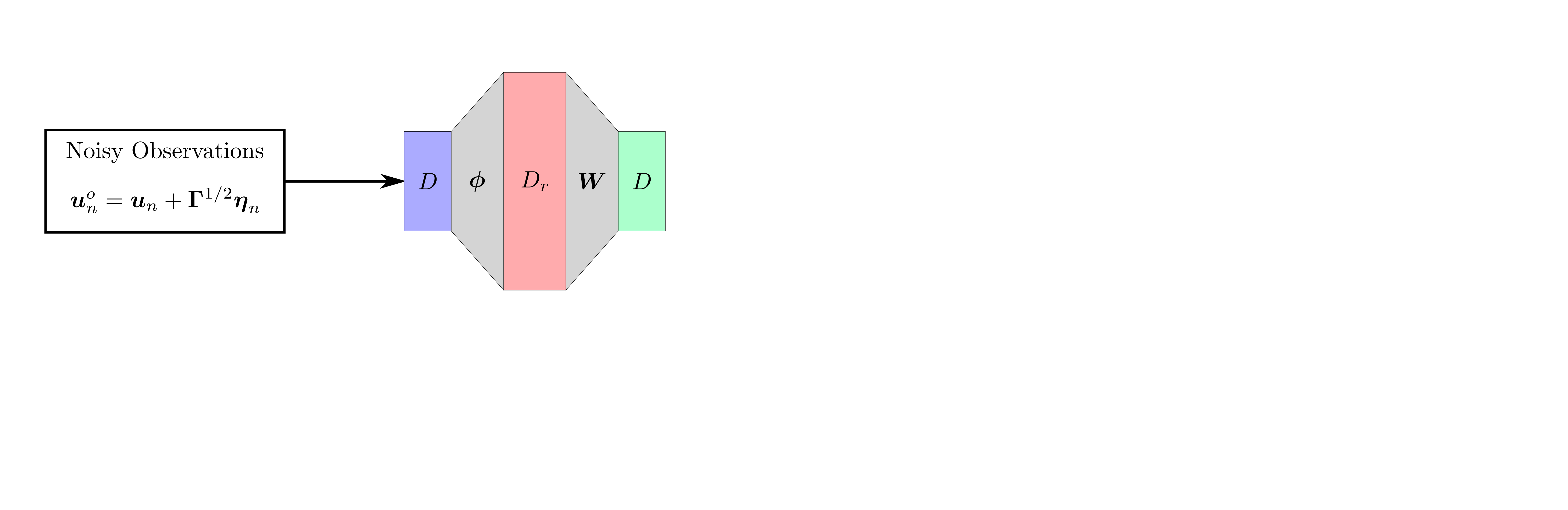 -- 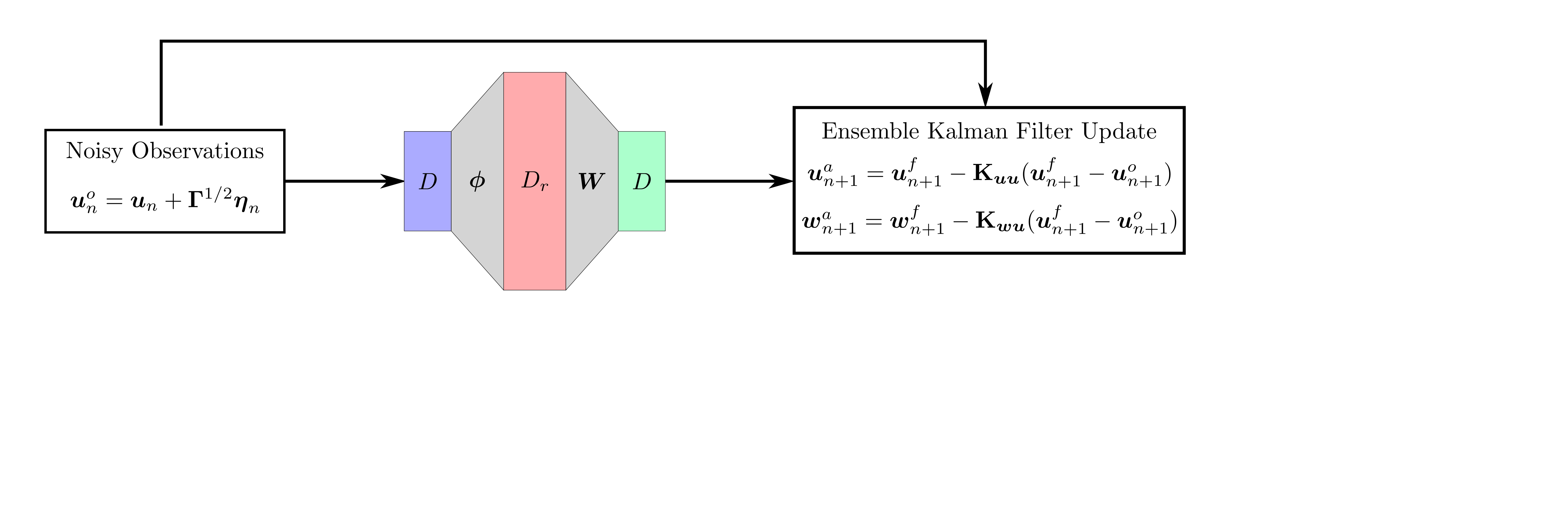 -- 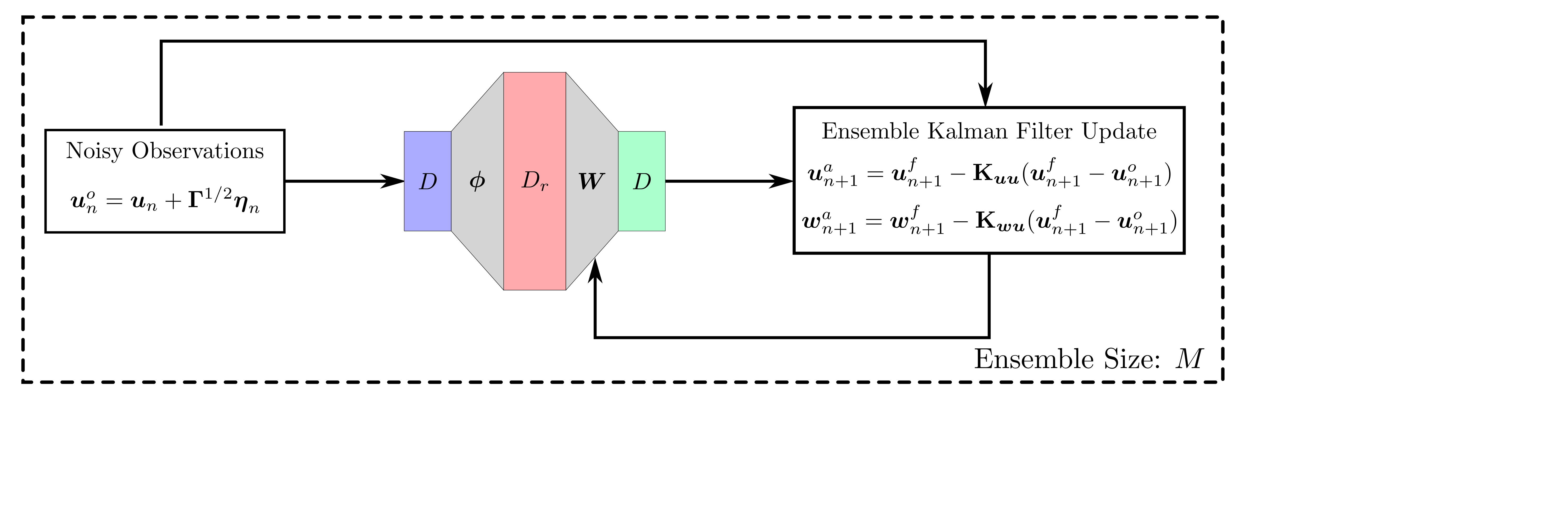 -- 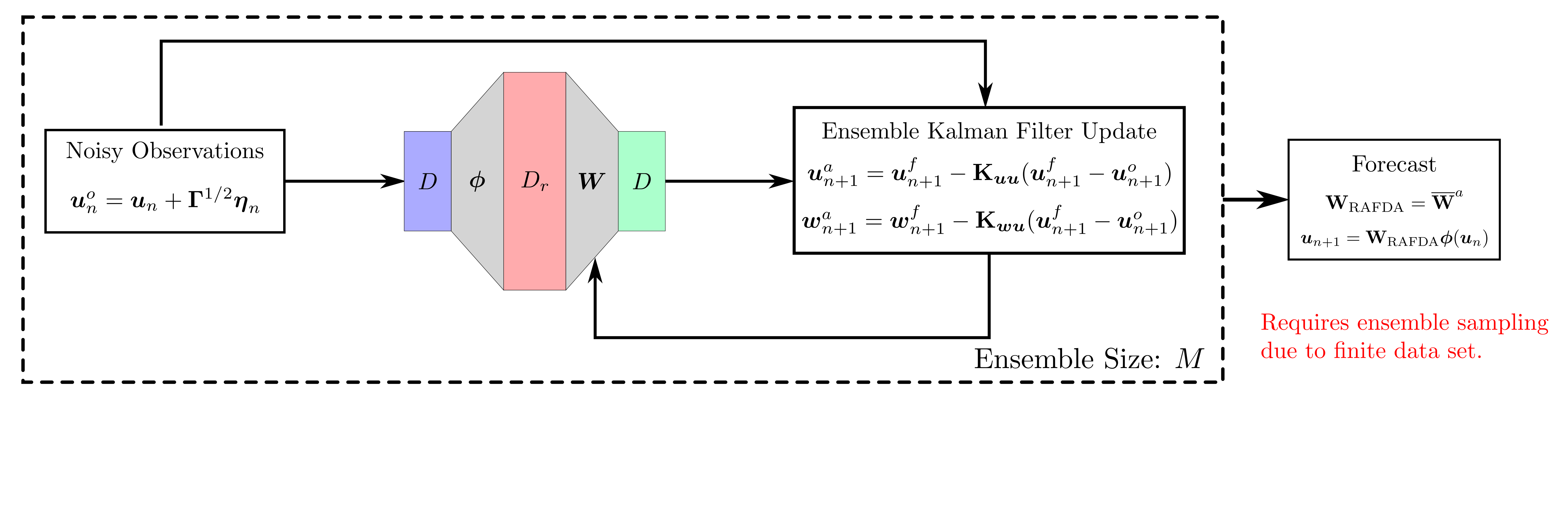 -- 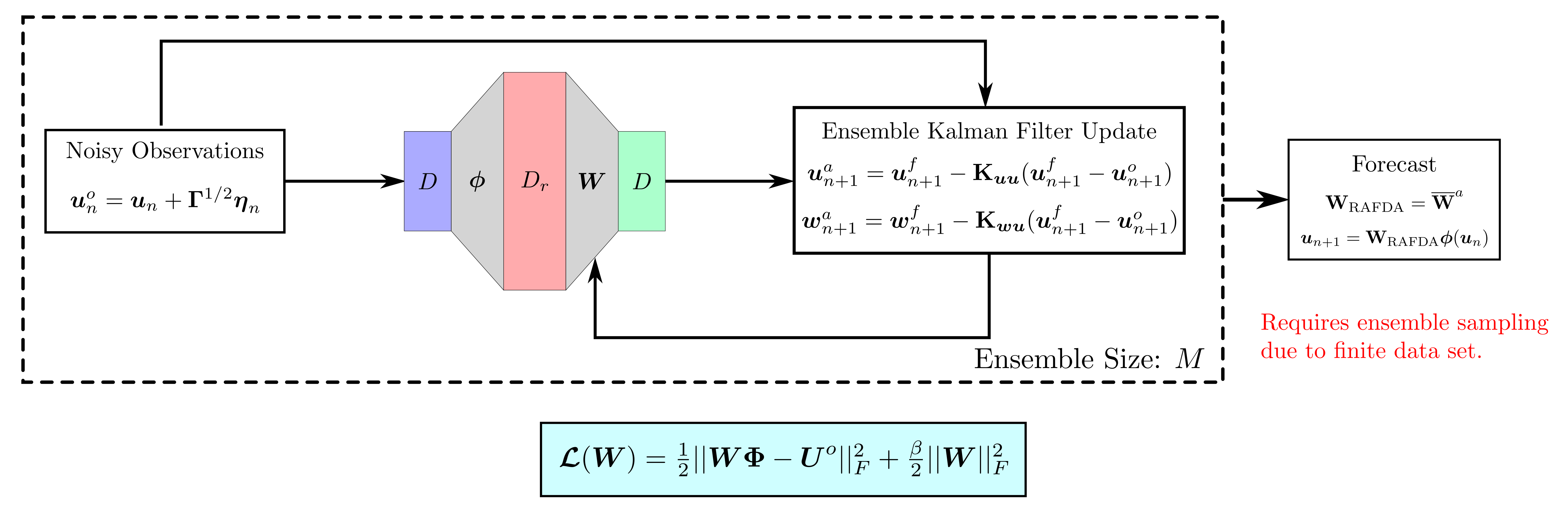 --- # Topological Data Assimilation  ??? For my second application of persistence optimization that I am actively working on I will utilize the concept of data assimilation to optimally combine measured and model results. I plan to utilize forecasting to obtain models from measurement data and apply persistence optimization to obtain an optimal forecast for the next assimilation window. This method will work by assuming that we have N sensor observations with additive noise. These measurements are then used for generating a forecast model using any of the methods I presented such as random feature maps. I will then compute persistence on the measurement data (potentially 0D and 1D) and compute persistence on the forecast model. Using the wasserstein distance, the dissimilarity between these two diagrams can be quantified and persistence optimization can be used to minimize the wasserstein distance between them. This will give a new forecast model that has a persistence diagram that is closer to the observation persistence diagram. The new forecast makes up the analysis which is fed back into the loop to be used as the model in the next assimilation window and the original model is used to make a new prediction and the process is continued as new observations stream in. Specifically, my goal here is to perform data assimilation using the wasserstein distance between the model and expected persistence diagrams. -- 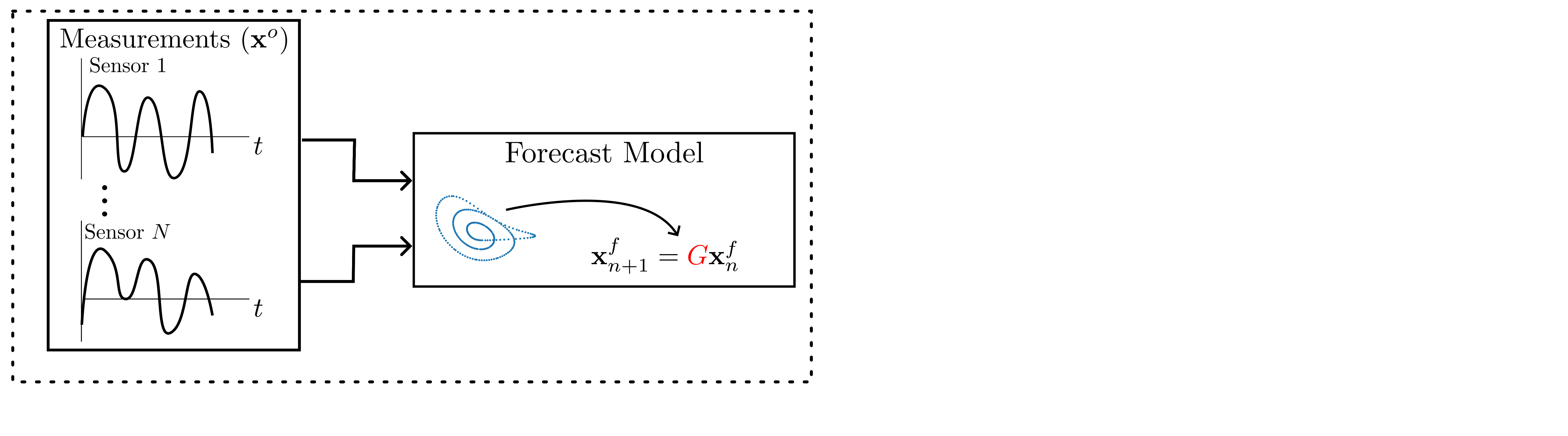 -- 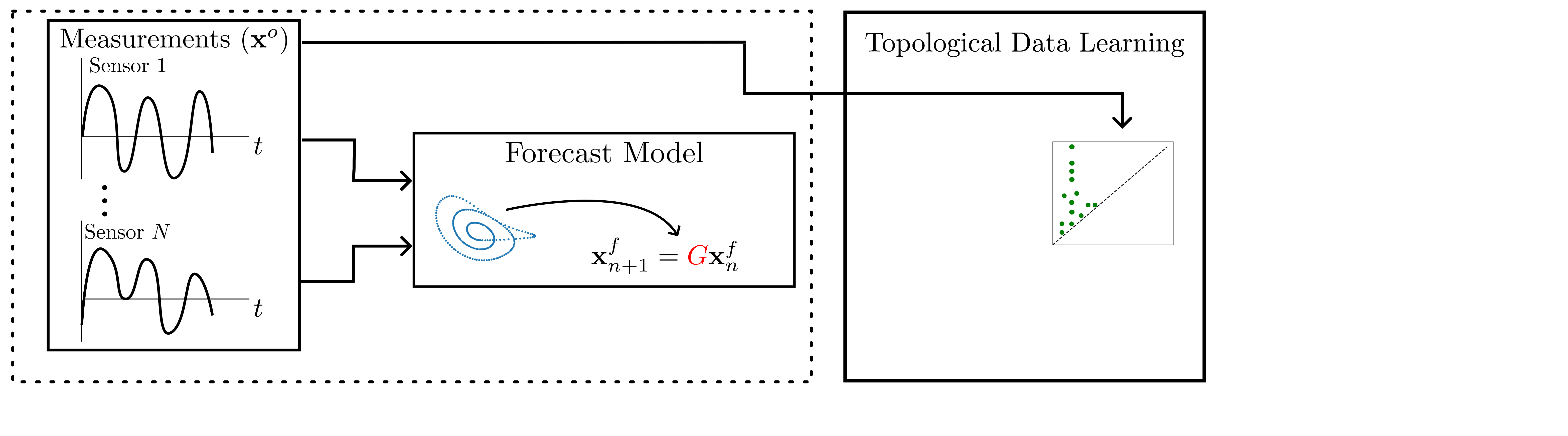 -- 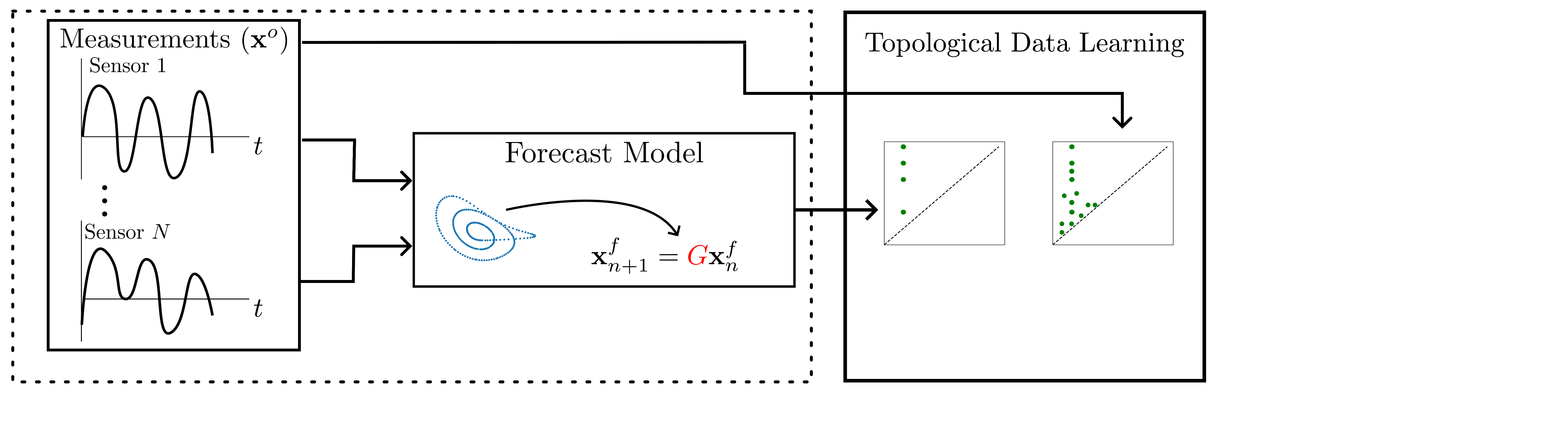 --  --  --  --  --  --- # Preliminary Results (Target Persistence Diagrams) - `\(\mathcal{L} = W(PD_m^1, PD_t^1)\)` - `\(PD_m\equiv\)` Measured Persistence Diagram - `\(PD_t\equiv\)` Target Persistence Diagram  ??? Here I will show an example of using persistence optimization with the wasserstein distance as preliminary results. If we start with this point cloud and imagine that it is the model forecast with the 1D persistence diagram consisting of the red points. If the observation persistence diagram is the green point, the observations would be a single loop in the point cloud space with no noise. The goal is to minimize the wasserstein distance to get a point cloud with a similar persistence diagram. Here is the animation for this process. We see that the point cloud expands and the persistence pair approaches the target persistence diagram minimizing the wasserstein distance. Now if the observations contain noise, the noise will show up in the persistence diagram as pairs near the diagonal. For example if this was our target persistence diagram we can see how the optimization performs in this case. While the persistence diagrams do not exactly match here, the optimization still moved the significant persistence pair very close to the target. This process learns the most significant topological features for the point cloud from the target persistence diagram but avoids overfitting by finding a local minimum in the cost function instead of the global minimum at zero. These results suggest that this method will be successful in a data assimilation framework because the noise will be effectively filtered from the observations. --  --  --  --- # Preliminary Results ( Periodic Lorenz System) - `\(\mathcal{L} = W(PD_m^1, PD_t^1) + W(PD_m^0, PD_t^0)\)` - `\(PD_m\equiv\)` Measured Persistence Diagram - `\(PD_t\equiv\)` Target Persistence Diagram  ??? I then extended the preliminary results to use noisy observations from a dynamical system. Here I simulated the periodic lorenz system and added some noise to the signal. If we want an optimal combination of the model and observations the 0D and 1D persistence diagrams can be used to optimally perturb the model results and allow some of the topological structure to flow from the measurements to the model. Note I am only showing the 1D persistence diagram here for clarity. In this animation we see that the model results slightly expand to reach a persistence diagram that is close to the measurements but does not directly learn all of the noise in the original point cloud. --  --- # Preliminary Results ( Chaotic Lorenz System) - `\(\mathcal{L} = W(PD_m^1, PD_t^1) + W(PD_m^0, PD_t^0)\)` - `\(PD_m\equiv\)` Measured Persistence Diagram - `\(PD_t\equiv\)` Target Persistence Diagram  ??? I also performed this process for the chaotic lorenz system here. In the animation here, we see that the model results are perturbed slightly to combine the results. The next step will be to perform this process using a forecasting model and perform the optimization iteratively as new measurements and predictions stream in. --  --- # Time Series Representations  ??? In many engineering problems, it is only possible to measure one state of the system. For example only having the ability to directly measure angular frequency of a pendulum. For chapter two of my talk, I will discuss advancements I have contributed to in the area of estimating time series embedding parameters and time series network representations using TDA. --- class: inverse # Related Publications <br> - Myers, A. D., **Chumley, M. M.**, & Khasawneh, F. A. (2024). Delay Parameter Selection in Permutation Entropy Using Topological Data Analysis. *Under Review* <br> - Myers, A. D., **Chumley, M. M.**, Khasawneh, F. A., & Munch, E. (2023). Persistent homology of coarse-grained state-space networks. Physical Review E, 107(3), 034303. ??? Here are my relevant publications for this chapter. --- # Takens Embedding  ??? In the case where only one state of a system can be measured, the standard practice is to apply a Takens delay embedding to attempt to reconstruct the full attractor. The way it works is a delay and dimension are chosen and the delayed states are used to represent the unmeasured states of the system. In this example here the dimension is 3 so we take the signal at time t, t+tau and t+2tau and plot those coordinates in 3D space. Doing this results in a reconstructed attractor for the system that Takens' proved is topologically equivalent to the original attractor assuming the correct delay and dimension are chosen. If the chosen delay is too small, the reconstructed attractor will not have the correct topology because all of the states will be close to the hyperdiagonal. --- # Classical Embedding Delay Selection  <!-- -- --> <!--  --> ??? Many methods have been developed to automatically select a delay from a given time series such as the first minimum of the average mutual information. However, these methods are not guaranteed to work and it may be difficult to choose thresholds and hyperparameters to get an optimal delay. --- # Embedding Parameter Estimation  ??? This leads to my work on embedding delay estimation for attractor reconstruction where I will show how the embedding delay can be estimated using TDA. --- # Sublevel Persistence  ??? The methods for this section require using sublevel persistent homology but on a 1 dimensional signal this time. I am showing an animation of how this works in one dimension here for completeness but it is the exact same concept as the image but we can only consider 0D persistence for a 1D signal. --- # Time Domain Approach  .footnote[Myers, A. D., **Chumley, M. M.**, & Khasawneh, F. A. (2024). "Delay parameter selection in permutation entropy using topological data analysis." Under review.] ??? My first approach utilizes the time domain signal where I compute 0D sublevel persistence and obtain the time ordered lifetimes or death minus birth values from the persistence diagram. The times between adjacent lifetimes are labeled as Tbi. The associated frequencies for the system can be computed by the reciprocals of these times to get a distribution of frequencies in the system. For a periodic signal the maximum significant frequency can be directly observed from this distribution. For a chaotic signal it is much more difficult to determine the significant frequencies. To automate the process when the signal is chaotic or if noise is present, the 75% quantile of the frequency distribution is taken to allow for some outliers and the delay is taken to be the reciprocal of that frequency. --  --- # Results (Rossler)  .footnote[Myers, A. D., **Chumley, M. M.**, & Khasawneh, F. A. (2024). "Delay parameter selection in permutation entropy using topological data analysis." Under review.] ??? Here are some results from the time domain approach. Using the periodic and chaotic rossler system this method gives a delay of 23 and the suggested delay for this system in the literature is 9. The delay of 23 gives a more optimal attractor reconstruction whereas the smaller delay is skewed along the diagonal. I also have a method for estimating the delay using persistence on the frequency domain that is in the paper at the bottom. --- # Coarse-Grained State Space Network  ??? For my final topic of this chapter I will breifly show how I used persistent homology to perform dynamic state detection on network representations of time series signals. --- # Pipeline  .footnote[Myers, A. D., **Chumley, M. M.**, Khasawneh, F. A., & Munch, E. (2023). "Persistent homology of coarse-grained state-space networks." Physical Review E, 107(3), 034303.] ??? I don't have time to cover these results in detail but I will show the pipeline to give a general idea. When analyzing a timeseries, many times it is easy for a human to distinguish a periodic signal from a chaotic one. However, characterizing these states automatically can be computationally expensive. A common approach for improving the efficiency of this process is to represent the timeseries as a network. In this pipeline there are three methods for doing this, using a takens embedding to reconstruct the attractor, sequences of ordinal patterns and coarse graining of the state space which is the method I focused on. These approaches all result in a network representation of the signal. My goal was to study the topology of the coarse grained state space network for state identification and I did this by obtaining a distance matrix using the distance metrics discussed earlier for the networks and then I obtained the persistence diagrams. The persistent diagrams were then used for determining the dynamic state of the signal. --  --  --  --  --- # Texture Analysis  ??? Now I will breifly show some of my other work that I did not have time to present today. The first project was performing texture analysis using TDA. --- class: inverse count: false # Related Publications <br> - **Chumley, M. M.**, Yesilli, M. C., Chen, J., Khasawneh, F. A., & Guo, Y. (2023). Pattern characterization using topological data analysis: Application to piezo vibration striking treatment. Precision Engineering *[Editor's Recommendation]*, 83, 42-57. <br> - Yesilli, M. C., **Chumley, M. M.**, Chen, J., Khasawneh, F. A., & Guo, Y. (2022, June). Exploring surface texture quantification in piezo vibration striking treatment (PVST) using topological measures. In International Manufacturing Science and Engineering Conference (Vol. 85819, p. V002T05A061). American Society of Mechanical Engineers. ??? Here are my publications on this work. --- # Texture Analysis Overview 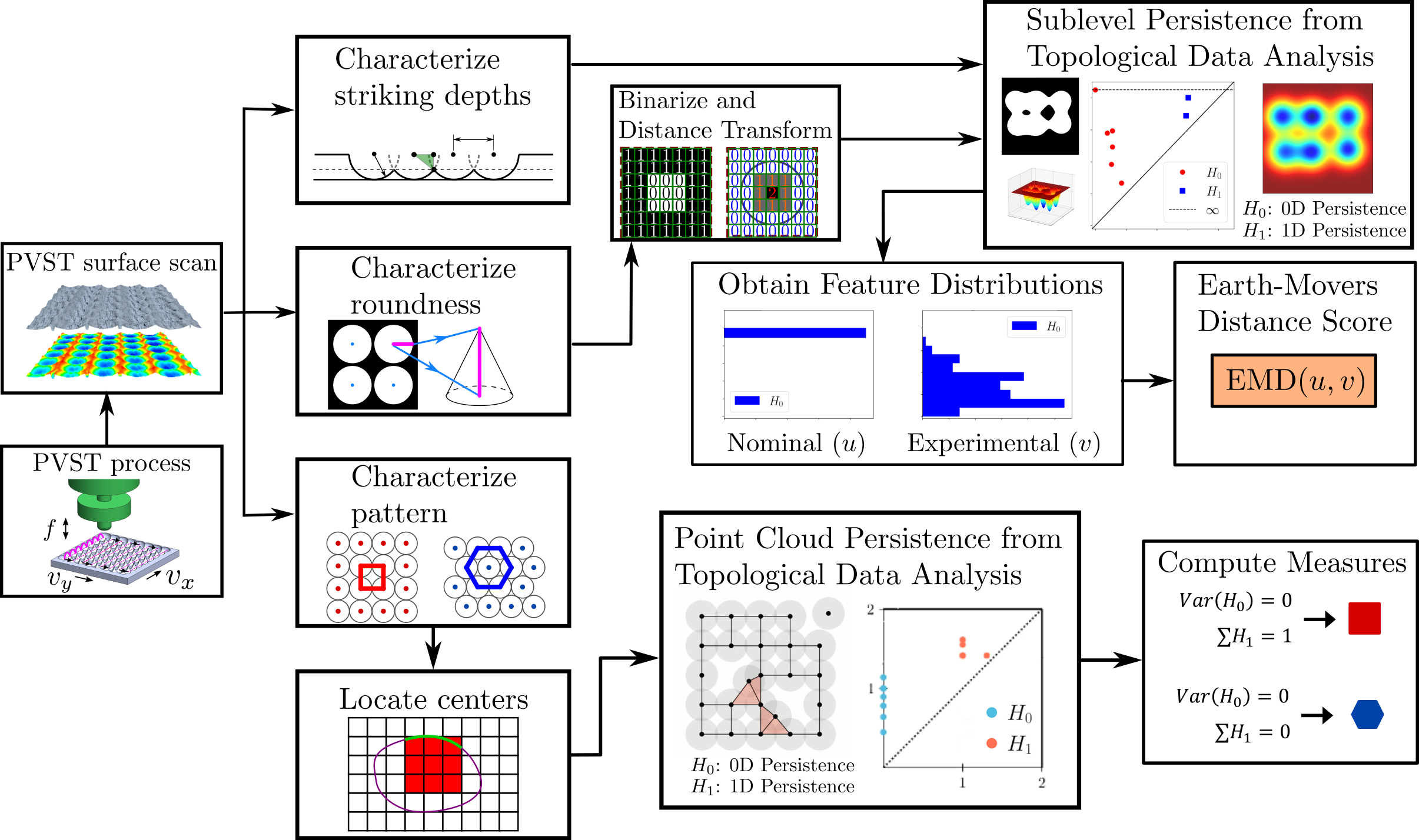 ??? I was given data from a manufacturing process called piezo vibration striking treatment where a texture is intentionally produced on a surface to improve its mechanical properties. I analyzed the PVST scans using TDA to quantify three different features of the texture. I characterized the strike depths, roundness, and pattern shapes all using TDA with this pipeline and developed scores to provide the user with a measure of consistency in these features. --- # Metabolic Oscillations 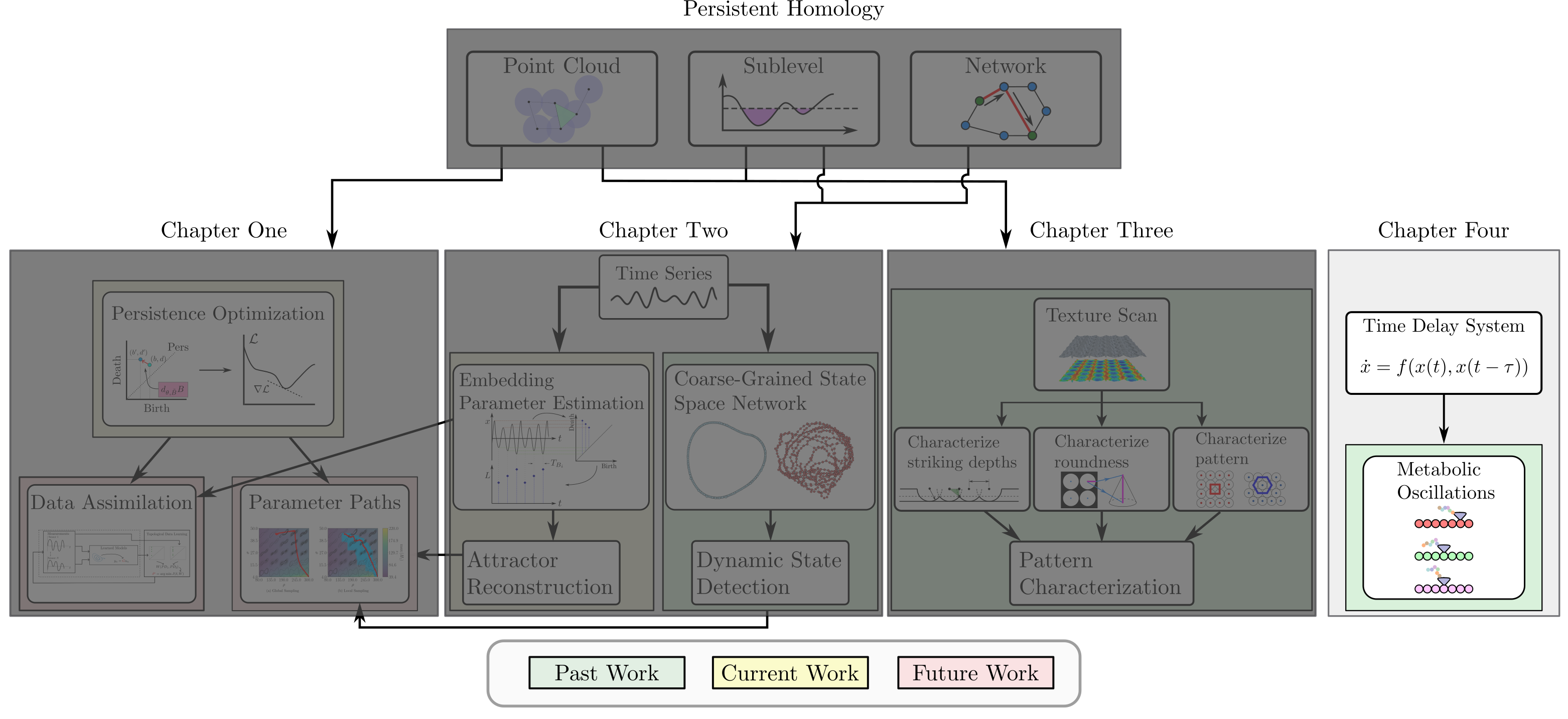 ??? For the last project I will discuss is my work on a nonlinear delay model for metabolic oscillations in yeast cells. --- class: inverse count: false # Related Publications <br> - **Chumley, Max M.**, Khasawneh, F.A., Otto, A., Gedeon, T. (2023). ``A Nonlinear Delay Model for Metabolic Oscillations in Yeast Cells." Bulletin of Mathematical Biology, 85, 122. ??? Here is my paper introducing the model. --- # Metabolic Oscillations  ??? When yeast cells are starved of resources, it has been observed experimentally that the protein production rates will oscillate in approximately 40 minute intervals. I developed a time delay framework for modeling metabolic oscillations in yeast cells and analyzed the model using three numerical approaches to find parameters that resulted in a limit cycle. I also extended the model to include three coupled proteins and used the same methods for analysis. --  --- count: false # Metabolic Oscillations 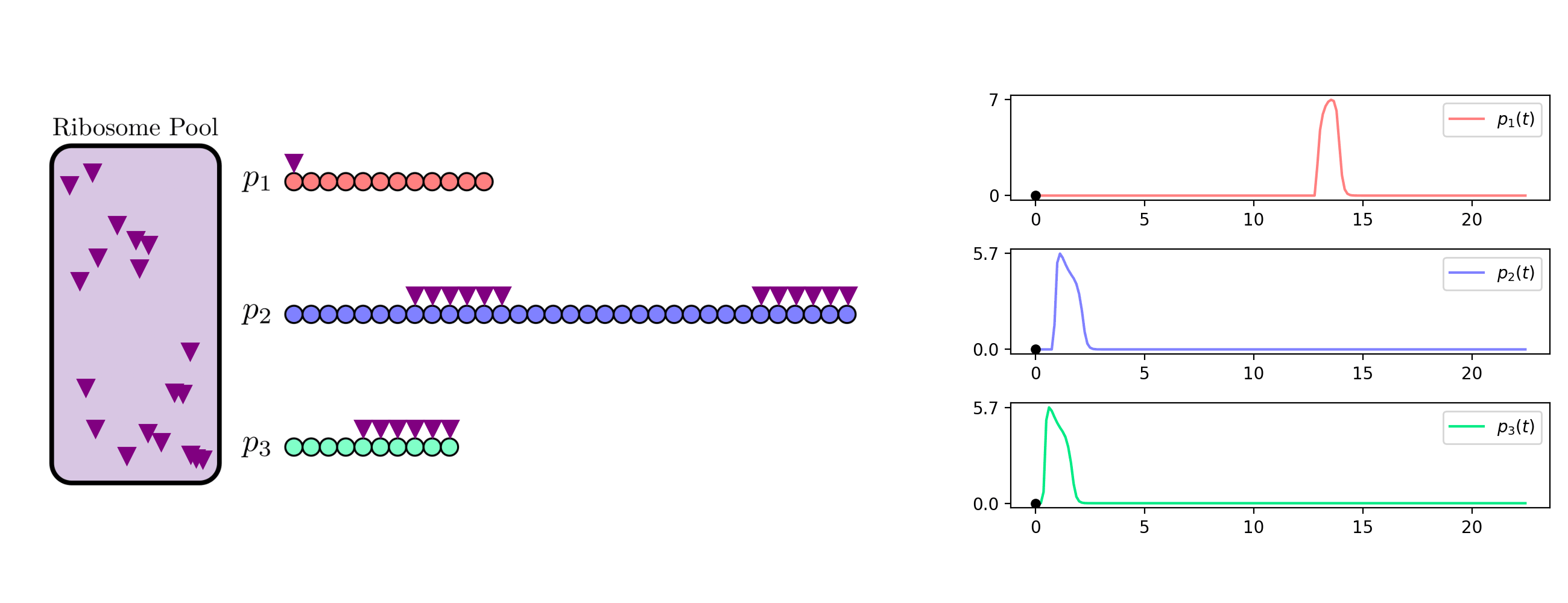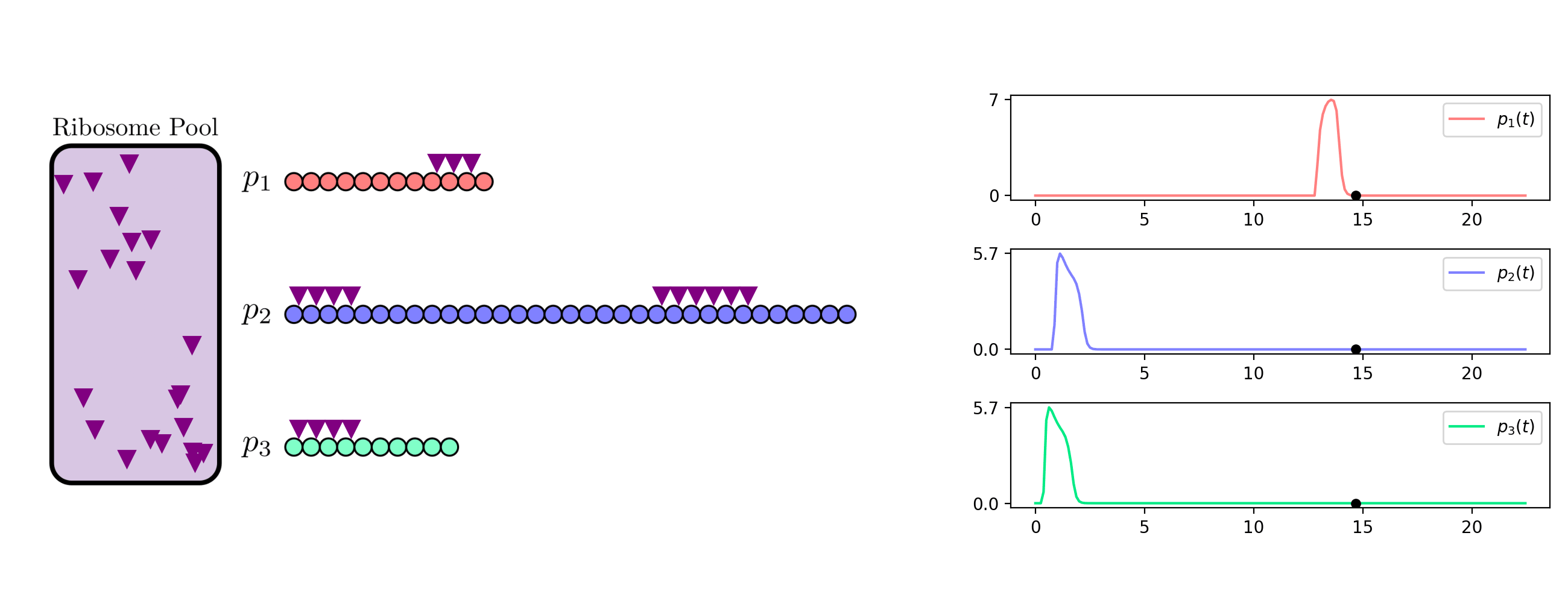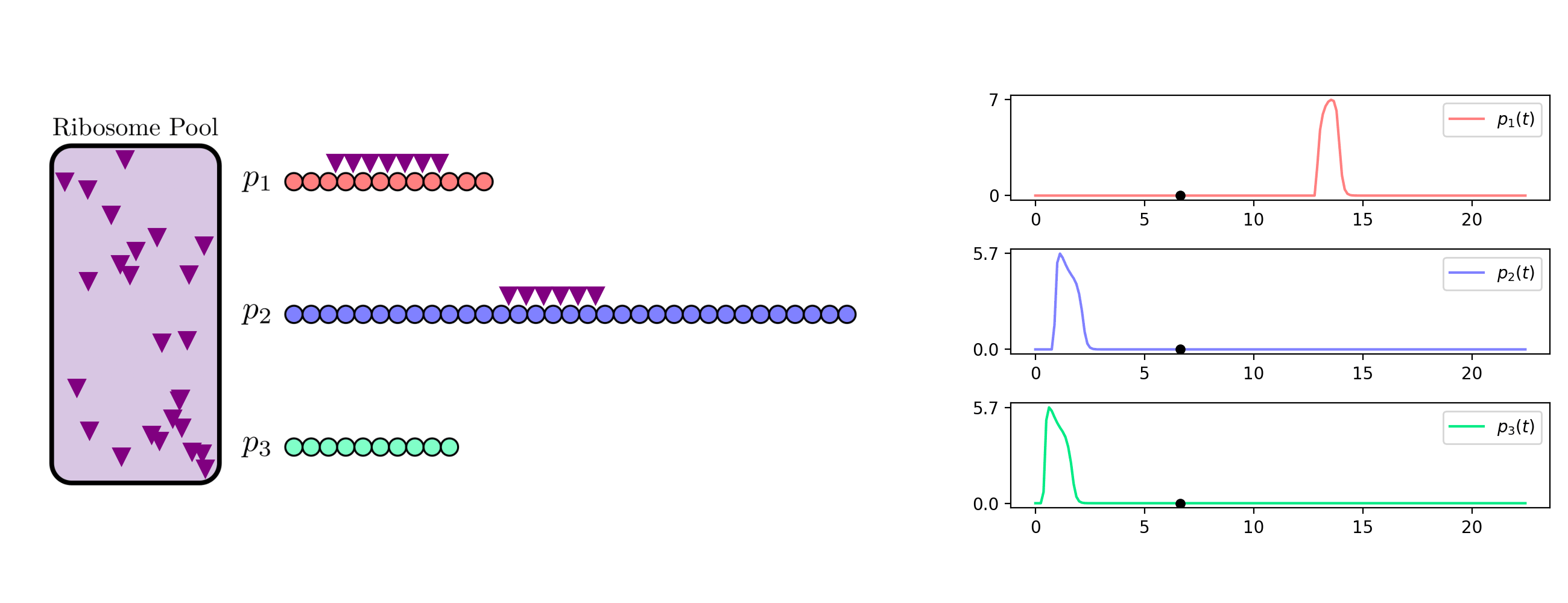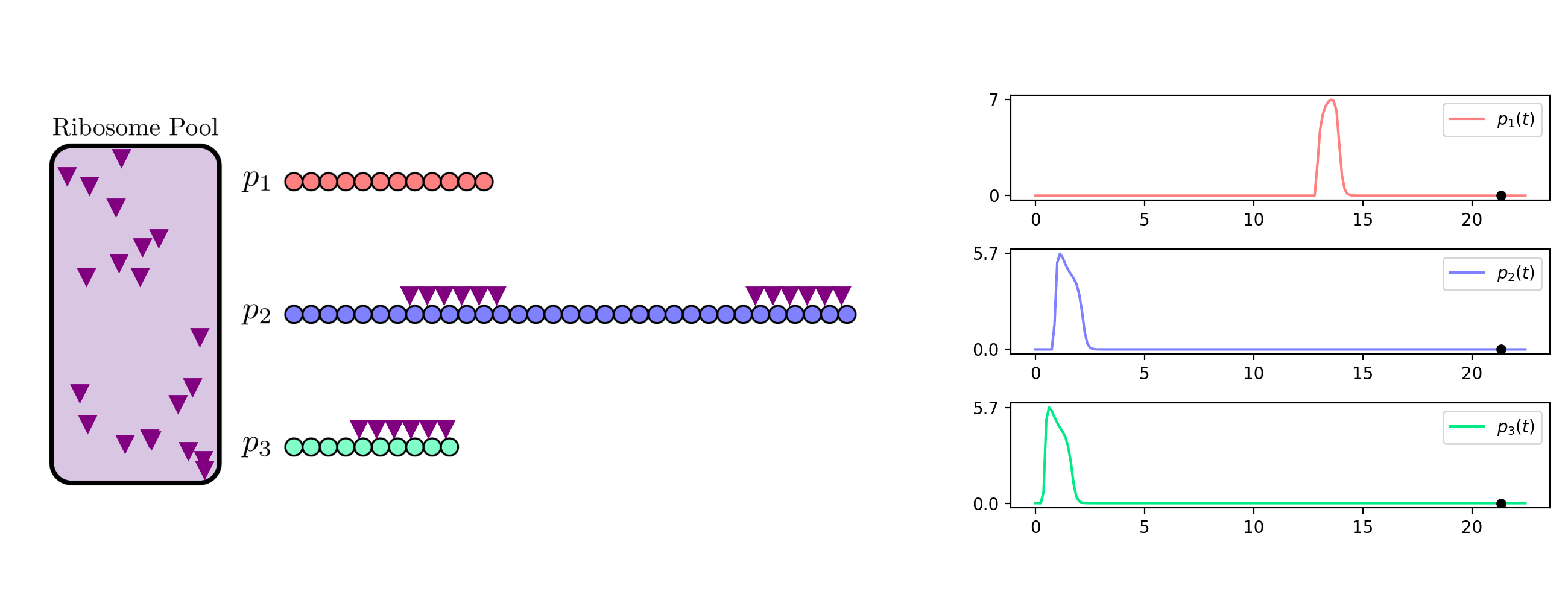 .footnote[**Chumley, M.M.**, Khasawneh, F.A., Otto, A. et al. "A Nonlinear Delay Model for Metabolic Oscillations in Yeast Cells". Bull. Math Biol. 85, 122 (2023). https://doi.org/10.1007/s11538-023-01227-3] ??? I do not have time to show more results from this project, but one of the most significant results came from the 3 protein model where if the cell is starved of resources the oscillation peaks did not occur at the same time which I believe could be a more efficient use of resources for the cell. --- # Goal Summary  ??? Here is a summary of my proposed goals. I plan to develop a library of cost function terms to specify desired topological features for a data set for use with persistence optimization. I will then use this cost function library to develop algorithms for propagating the gradient through a pipeline that includes a dynamical systems parameter space to perform optimal parameter space navigation. I plan to apply these tools to hall effect thruster data from my internship for experimental validation. My last goal is to utilize persistence optimization to develop a topological data assimilation framework using the wasserstein distance between persistence diagrams. Here is a gantt chart for my graduation plan. I plan to mainly focus on developing the data assimilation framework prior to my internship over the summer. In the fall I will be pushing the parameter space optimization goals and I plan to defend my thesis in the spring of 2025. --  -- 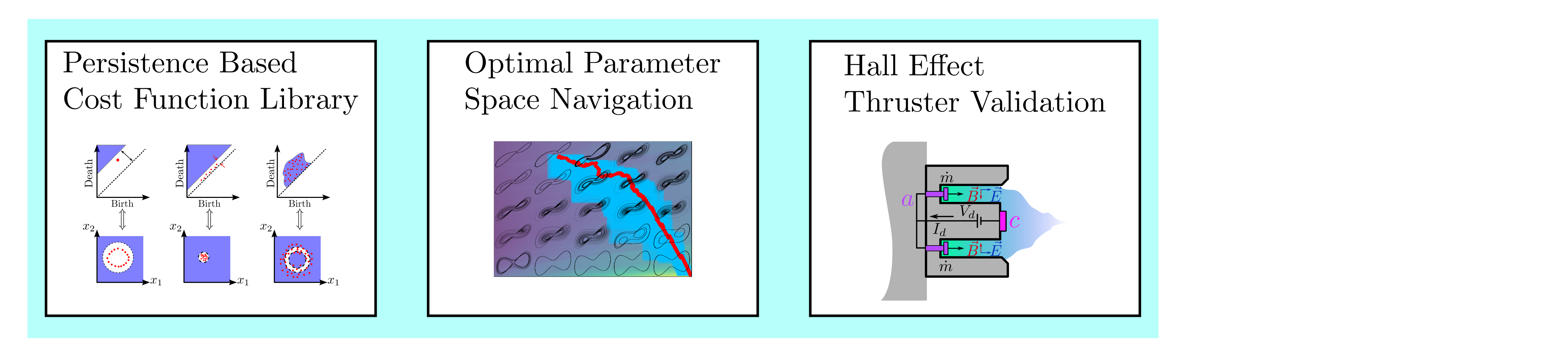 -- 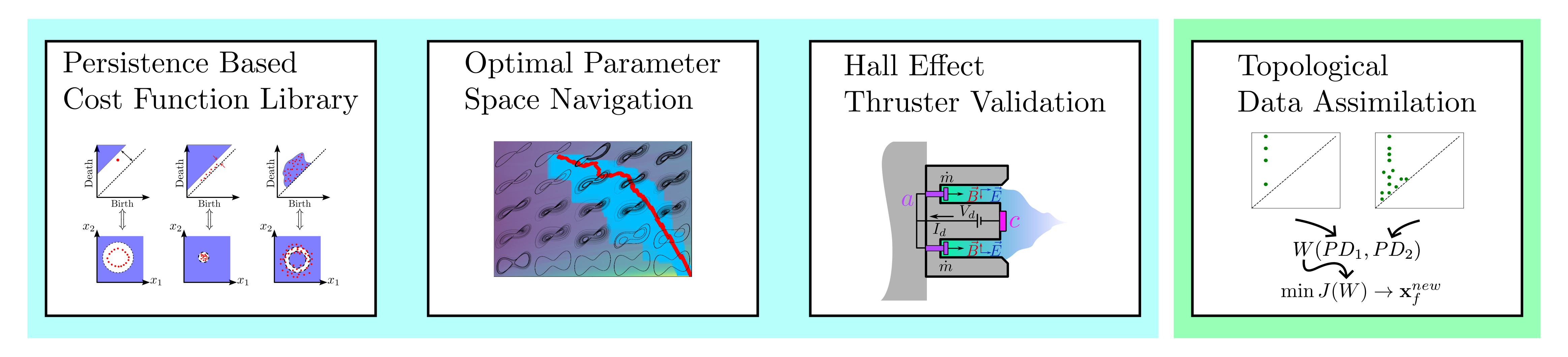 -- 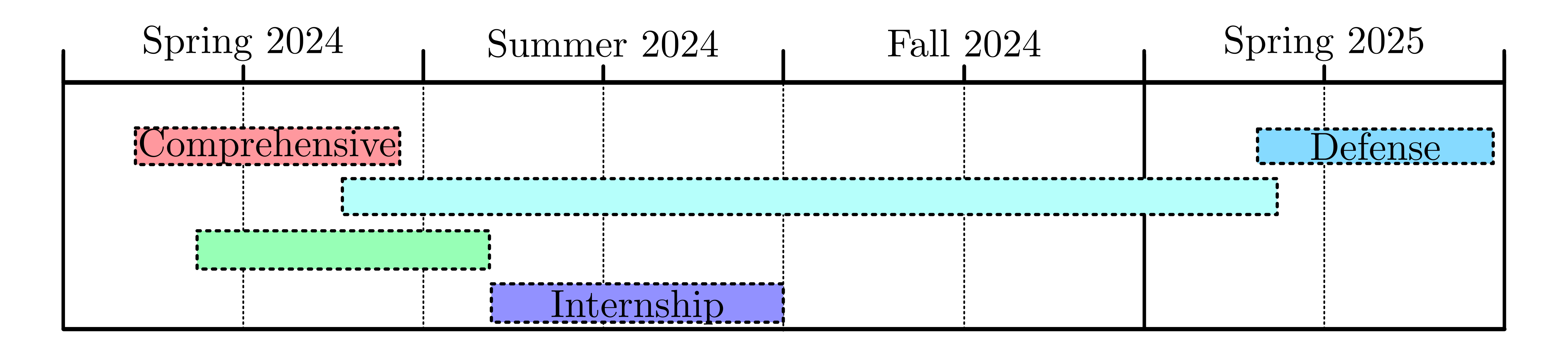 --- # Thank you!  .footnote[ <p style="font-size: 15px;">1. <b>Chumley, M.M.</b>, Yesilli, M.C., Chen, J, Khasawneh, F. A., & Guo, Y., <b>"Pattern characterization using topological data analysis: Application to piezo vibration striking treatment"</b>, Precision Engineering, Volume 83, 2023. <i>[Editor's Recommendation]</i></p> <p style="font-size: 15px;">2. Yesilli, M.C., <b>Chumley, M.M.</b>, Chen, J, Khasawneh, FA, & Guo, Y. <b>"Exploring Surface Texture Quantification in Piezo Vibration Striking Treatment (PVST) Using Topological Measures.”</b> Proceedings of the ASME 2022 17th International Manufacturing Science and Engineering Conference.</p> <p style="font-size: 15px;">3. <b>Chumley, M.M.</b>, Khasawneh, F.A., Otto, A. et al. <b>"A Nonlinear Delay Model for Metabolic Oscillations in Yeast Cells"</b>. Bull Math Biol 85, 122 (2023). https://doi.org/10.1007/s11538-023-01227-3</p> <p style="font-size: 15px;">4. Myers, A. D., <b>Chumley, M. M.</b>, Khasawneh, F. A., & Munch, E. (2023). <b>"Persistent homology of coarse-grained state-space networks."</b> Physical Review E, 107(3), 034303.</p> <p style="font-size: 15px;">5. Myers, A. D., <b>Chumley, M. M.</b>,& Khasawneh, F. A. (2024). <b>"Delay parameter selection in permutation entropy using topological data analysis."</b> Under review.</p> ] ??? Thank you for your attention. You can find my papers and slides on my website maxchumley.com. My code is available on our teaspoon python library and I plan to implement more libraries for my future work on optimization. I also have mini tutorial content from the SIAM DS mini tutorial on topological signal processing that I helped organize and present last year. The git repo can be accessed with the QR code. Are there any questions?